Let's do some calculus! (29)
x → 0 lim x 4 ( e 2 x 4 − 2 x 4 − 1 ) sin x 4 − x 4 cos x 4 + x 2 0 = ?
Submit your answer rounded up to 3 places of decimal.
Notation: e ≈ 2 . 7 1 8 2 8 is the Euler's number .
For more problems on calculus, click here .
The answer is 0.167.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I don't really know the application of the 'big O O ( ⋅ ) ' notation that you've used in your solution. I've seen them on Wikipedia but don't know what are they.
Log in to reply
In this case, O ( x 1 2 ) = a 3 x 1 2 + a 4 x 1 6 + a 5 x 2 0 + . . . .
Log in to reply
Can you refer me some good link for me to understand this?
We can Put t = x 4 to reduce calculations
Really tedious solution using L'Hôpital's rule brute force
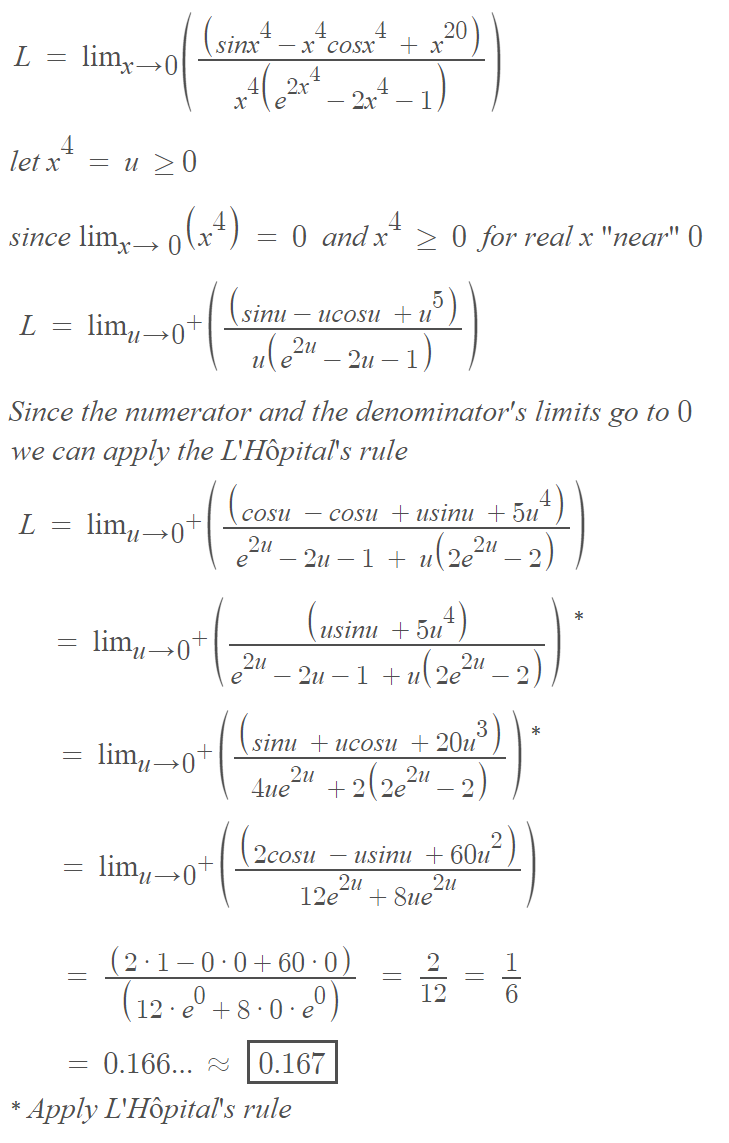
L = x → 0 lim x 4 ( e 2 x 4 − 2 x 4 − 1 ) sin x 4 − x 4 cos x 4 + x 2 0 = x → 0 lim x 4 ( 1 + 1 ! 2 x 4 + 2 ! 4 x 8 − . . . − 2 x 4 − 1 ) x 4 − 3 ! x 1 2 + 5 ! x 2 0 − . . . − x 4 ( 1 − 2 ! x 8 + 4 ! x 1 6 − . . . ) + x 2 0 = x → 0 lim 2 ! 4 x 1 2 − 4 ! 8 x 1 6 + O ( x 2 0 ) ( 2 ! 1 − 3 ! 1 ) x 1 2 − ( 4 ! 1 − 5 ! 1 + 1 ) x 2 0 + O ( x 2 4 ) = x → 0 lim 2 − 3 x 1 6 + O ( x 8 ) 3 1 − 3 0 3 1 x 8 + O ( x 1 2 ) = 6 1 ≈ 0 . 1 6 7 Using Maclaurin series Divide up and down by x 1 2