Let's do some calculus! (36)

Classical Mechanics Level 5

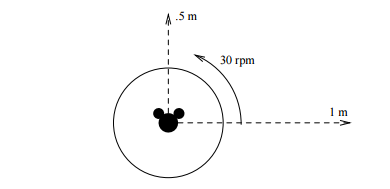
A mouse is sitting in a toy car on a negligibly small turntable. The car cannot turn on its own, but the mouse can control when the car is launched and when the car stops (the car has brakes). When the mouse chooses to launch, the car will immediately leave the turntable on a straight trajectory at 1 m / s 1 \ {m}/{s} .

Someone turns on (spins) the turntable and it spins at 30 r p m 30 \ rpm . Consider the set S S of points the mouse can reach in his car within 1 second 1 \ \text{second} after the turntable is set in motion. The car will travel in a straight line in the direction that it is facing. Just for clarity, the arrows in the figure below represent two possible paths the mouse can take.

What is the area of S S , in square meter(s)?

For more problems on calculus, click here .
π 3 \dfrac{\pi}{3} π 4 \dfrac{\pi}{4} π 2 \dfrac{\pi}{2} π 8 \dfrac{\pi}{8} π 6 \dfrac{\pi}{6}

Tapas Mazumdar by Tapas Mazumdar , 20, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Jon Haussmann
Oct 31, 2016

Suppose the mouse launches at an angle of θ \theta from its original direction. It took a time of t = θ / π t = \theta/\pi to get there, and when it launches, it can reach a distance of up to r = 1 − t = 1 − θ / π r = 1 - t = 1 - \theta/\pi . Therefore, the area of S S is ∫ 0 π ( 1 − θ / π ) 2 2 d θ = π 6 . \int_0^\pi \frac{(1 - \theta/\pi)^2}{2} \ d \theta = \frac{\pi}{6}.

4 Helpful 0 Interesting 0 Brilliant 0 Confused

Did the same!!!

Aaron Jerry Ninan - 4 years, 4 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...