Let's fold a semicircle!
A semicircle was folded around the cord just like in the figure, knowing that and what is the value of ?
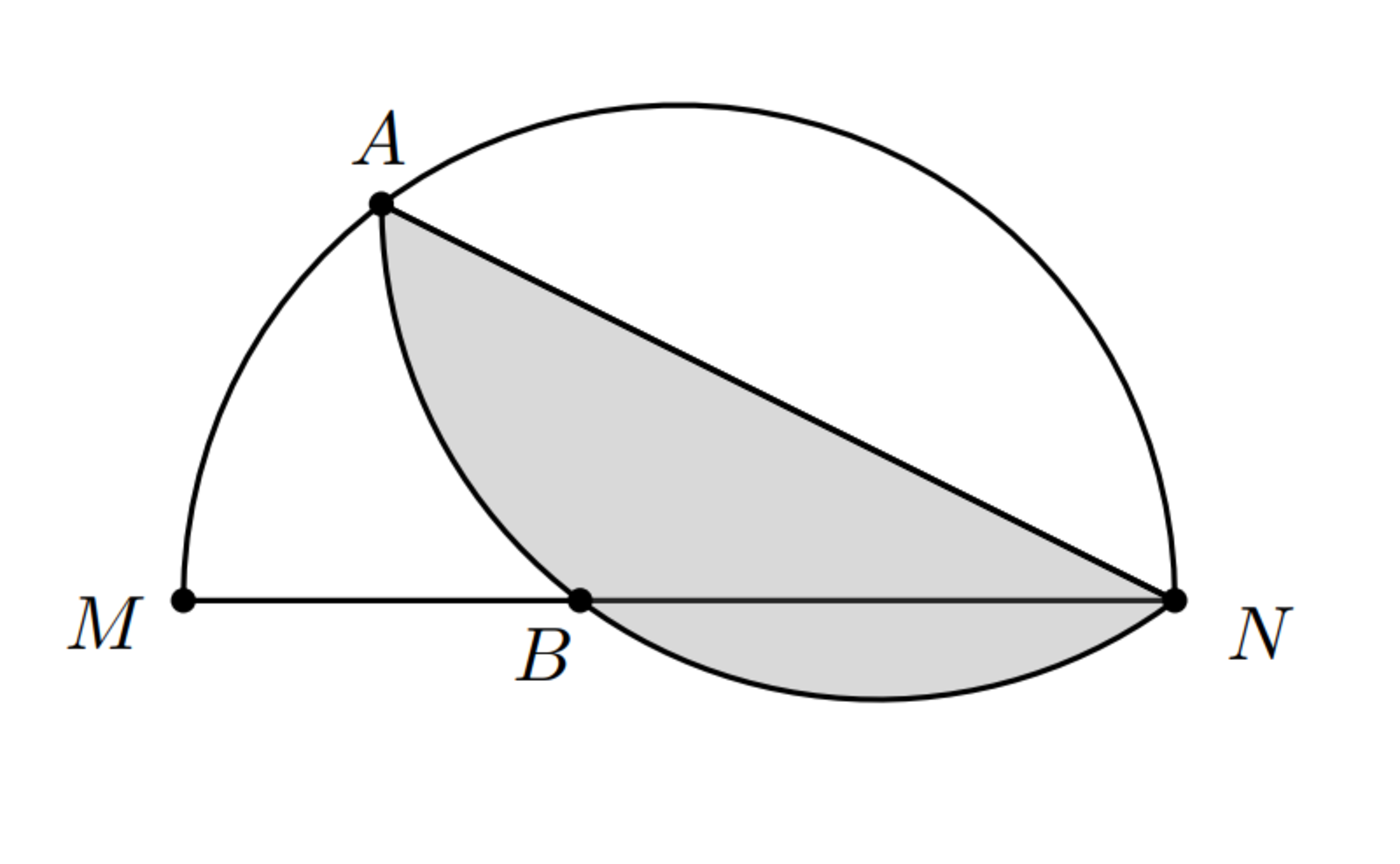
The answer is 80.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
OBS: ∠ M A N = 9 0 °
It can proved that A M = A B by reflecting △ A B N around A N (we know that B' will lie on the circuference because we are "unfolding" △ A B N
set the reflection of B = B ′
Now with the fact that ∠ A N M = ∠ B ′ N A so A B = A B ′ = A M (equal angles inscribed subtend a cord of same lenght).
(I don't know if this method is the most practic to find AN^2) Then drop the height from point A and let the square of the height be z also M A 2 = y , A N 2 = x
1 0 0 z = x y
x + y = 1 0 0 ,
z + ( 2 + 6 ) 2 = z + 6 4 = x
x = 8 0 = A N 2