Let's Get Numerical

Geometry Level 5

A parabola is tangent to the line y = 3 ( x + 2 ) y = \sqrt{3} (x + 2 ) and to the line y = − 1 2 ( x + 2 ) y = -\dfrac{1}{2} (x + 2) , and passes through the points ( 3 , − 1 ) , ( 5 , 11 ) (3, -1), (5, 11) (the green dots). Find the distance between the vertex of the parabola and its focus (the focal distance).


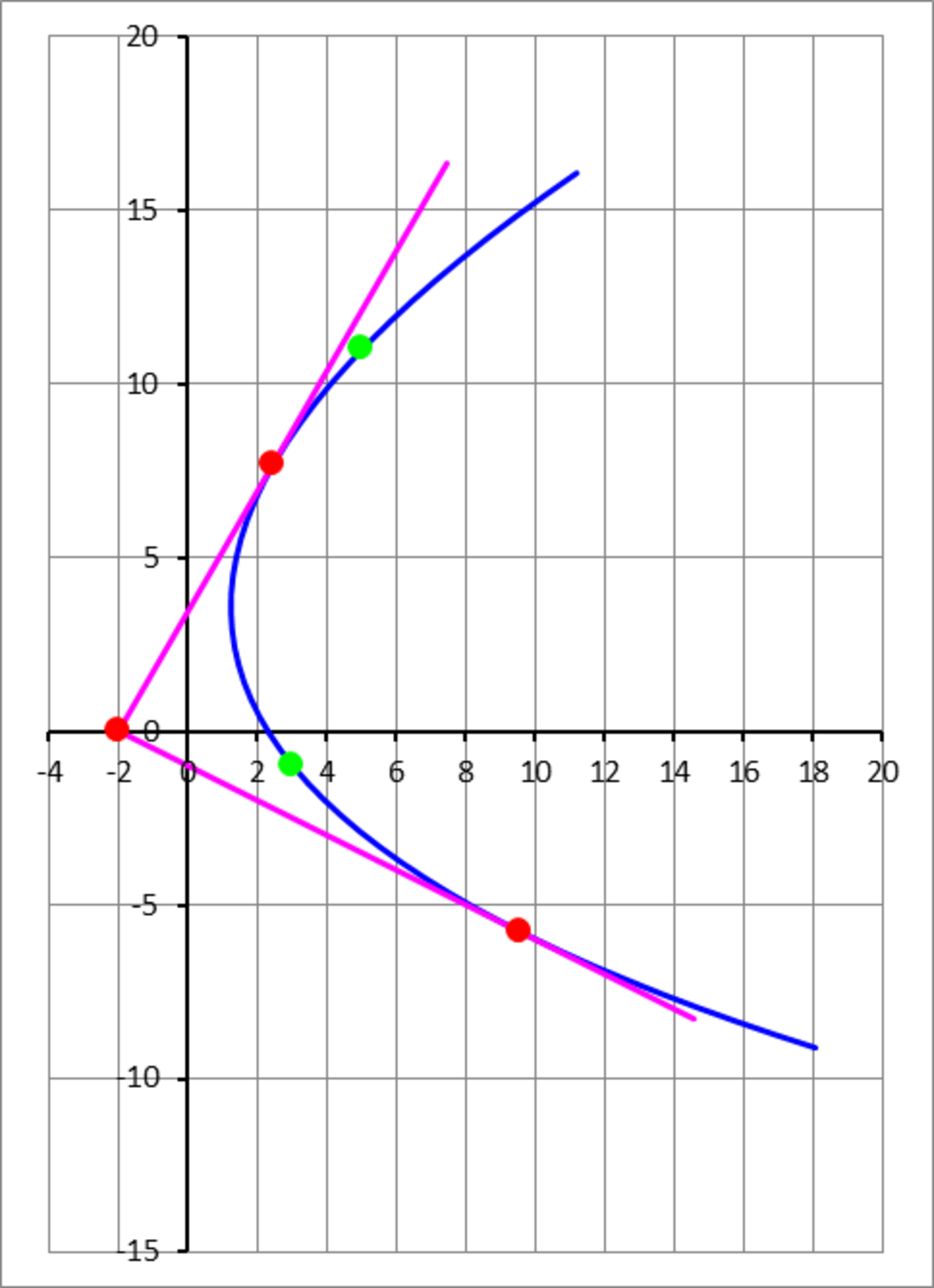
The answer is 3.1424.

Hosam Hajjir by Hosam Hajjir , 56, Canada

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Steven Chase
Jul 12, 2019

Let P ⃗ 0 \vec{P}_0 be the vertex location, and let u ⃗ 1 \vec{u}_1 and u ⃗ 2 \vec{u}_2 be orthogonal unit vectors which effectively define a new coordinate system. Define points ( x 1 , y 1 ) = ( 3 , − 1 ) (x_1,y_1) = (3, -1) and ( x 2 , y 2 ) = ( 5 , 11 ) (x_2,y_2) = (5,11) (the green points). The coordinates of a point on the parabola are:

P ⃗ = P ⃗ 0 + α u ⃗ 1 + a α 2 u ⃗ 2 x = x 0 + α u ⃗ 1 x + a α 2 u ⃗ 2 x y = y 0 + α u ⃗ 1 y + a α 2 u ⃗ 2 y u ⃗ 1 = ( cos ⁡ θ , sin ⁡ θ ) u ⃗ 2 = ( sin ⁡ θ , − cos ⁡ θ ) \vec{P} = \vec{P}_0 + \alpha \, \vec{u}_1 + a \, \alpha^2 \, \vec{u}_2 \\ x = x_0 + \alpha \, \vec{u}_{1x} + a \, \alpha^2 \, \vec{u}_{2x} \\ y = y_0 + \alpha \, \vec{u}_{1y} + a \, \alpha^2 \, \vec{u}_{2y} \\ \vec{u}_1 = ( \cos \theta, \sin \theta) \\ \vec{u}_2 = ( \sin \theta, -\cos \theta)

Each green point passed through has an associated α \alpha value. So the six unknowns are ( x 0 , y 0 , θ , a , α 1 , α 2 ) (x_0, y_0, \theta, a, \alpha_1, \alpha_2) . We need to solve six equations for the six unknowns. The first four have to do with the coordinates of the two green points passed through.

x 1 = x 0 + α 1 u ⃗ 1 x + a α 1 2 u ⃗ 2 x y 1 = y 0 + α 1 u ⃗ 1 y + a α 1 2 u ⃗ 2 y x 2 = x 0 + α 2 u ⃗ 1 x + a α 2 2 u ⃗ 2 x y 2 = y 0 + α 2 u ⃗ 1 y + a α 2 2 u ⃗ 2 y x_1 = x_0 + \alpha_1 \, \vec{u}_{1x} + a \, \alpha_1^2 \, \vec{u}_{2x} \\ y_1 = y_0 + \alpha_1 \, \vec{u}_{1y} + a \, \alpha_1^2 \, \vec{u}_{2y} \\ x_2 = x_0 + \alpha_2 \, \vec{u}_{1x} + a \, \alpha_2^2 \, \vec{u}_{2x} \\ y_2 = y_0 + \alpha_2 \, \vec{u}_{1y} + a \, \alpha_2^2 \, \vec{u}_{2y}

Consider the tangential intersection with the line y = 3 ( x + 2 ) y = \sqrt{3} (x + 2) . There should only be one corresponding α \alpha value. The quadratic equation for α \alpha should only have one solution. This gives us the fifth equation.

y = 3 ( x + 2 ) y 0 + α u ⃗ 1 y + a α 2 u ⃗ 2 y = 3 x 0 + 3 α u ⃗ 1 x + 3 a α 2 u ⃗ 2 x + 2 3 A = a u ⃗ 2 y − 3 a u ⃗ 2 x B = u ⃗ 1 y − 3 u ⃗ 1 x C = y 0 − 3 x 0 − 2 3 B 2 − 4 A C = 0 y = \sqrt{3} (x + 2) \\ y_0 + \alpha \, \vec{u}_{1y} + a \, \alpha^2 \, \vec{u}_{2y} = \sqrt{3} \, x_0 + \sqrt{3} \, \alpha \, \vec{u}_{1x} + \sqrt{3} \, a \, \alpha^2 \, \vec{u}_{2x} + 2 \sqrt{3} \\ A = a \, \vec{u}_{2y} - \sqrt{3} \, a \, \vec{u}_{2x} \\ B = \vec{u}_{1y} - \sqrt{3} \, \vec{u}_{1x} \\ C = y_0 - \sqrt{3} \, x_0 - 2 \sqrt{3} \\ B^2 - 4 A C = 0

We can do the same thing for the tangential intersection with the line y = − 1 2 ( x + 2 ) y = -\frac{1}{2} (x+2) , yielding the sixth equation.

y = − 1 2 ( x + 2 ) y 0 + α u ⃗ 1 y + a α 2 u ⃗ 2 y = − 1 2 x 0 − 1 2 α u ⃗ 1 x − 1 2 a α 2 u ⃗ 2 x − 1 A ′ = a u ⃗ 2 y + 1 2 a u ⃗ 2 x B ′ = u ⃗ 1 y + 1 2 u ⃗ 1 x C ′ = y 0 + 1 2 x 0 + 1 B ′ 2 − 4 A ′ C ′ = 0 y = -\frac{1}{2} (x+2) \\ y_0 + \alpha \, \vec{u}_{1y} + a \, \alpha^2 \, \vec{u}_{2y} = -\frac{1}{2} \, x_0 - \frac{1}{2} \, \alpha \, \vec{u}_{1x} - \frac{1}{2} \, a \, \alpha^2 \, \vec{u}_{2x} - 1 \\ A' = a \, \vec{u}_{2y} + \frac{1}{2} \, a \, \vec{u}_{2x} \\ B' = \vec{u}_{1y} + \frac{1}{2} \, \vec{u}_{1x} \\ C' = y_0 + \frac{1}{2} \, x_0 + 1 \\ B'^2 - 4 A' C' = 0

I used a genetic algorithm to solve (with mutation plus hybridization). The GA has better convergence than a pure hill-climbing algorithm (with mutation only). Its convergence is not as good as that of a multi-variate Newton-Raphson algorithm, but it is simpler to implement, given the complexity of the equations involved. The focal length is equal to 1 4 a \large{\frac{1}{4a}} , and it is approximately 3.14 3.14 . Approximate values for the other parameters are also given below. 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
 
###################################

Outputs
errsum = 0.00614021130147

x0 = 1.25682674784

y0 = 2.82365327969

theta = 96.8154994483

a = 0.0795505231975

alpha1 = -4.00335913139

alpha2 = 7.67404017138

f = 3.14265689214


###################################

Here is the Python code for the GA. Disclaimer: I'm not a programmer, so it probably looks pretty amateurish. 

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
 
import math
import random
import sys

####################################################################################################

# Code uses a genetic algorithm
# Approach uses a combination of mutation and hybridization

####################################################################################################

# Parameters from problem statement

x1 = 3.0
y1 = -1.0

x2 = 5.0
y2 = 11.0

rt3 = math.sqrt(3.0)
deg = math.pi/180.0

_2pi = 2.0*math.pi
pi = math.pi

####################################################################################################

# Start with a random array for each unknown parameter
# An "organism" is the set of values from all arrays corresponding to a particular address
# There are five organisms; the best two of which are bred at the end of each loop iteration
# The two "parents" spawn five new children

Matrix_x0 = [2.0*random.random(),2.0*random.random(),2.0*random.random(),2.0*random.random(),2.0*random.random()]
Matrix_y0 = [5.0*random.random(),5.0*random.random(),5.0*random.random(),5.0*random.random(),5.0*random.random()]

Matrix_theta = [pi*random.random(),pi*random.random(),pi*random.random(),pi*random.random(),pi*random.random()]

Matrix_a = [random.random(),random.random(),random.random(),random.random(),random.random()]

Matrix_alpha2 = [3.0*random.random(),3.0*random.random(),3.0*random.random(),3.0*random.random(),3.0*random.random(),]
Matrix_alpha1 = [-3.0*random.random(),-3.0*random.random(),-3.0*random.random(),-3.0*random.random(),-3.0*random.random(),]

err_sum_mtrx = [0.0,0.0,0.0,0.0,0.0]

####################################################################################################

for j in range(0,3000):
    for k in range(0,3000):                                # For each loop iteration - Here we have 9 million

        for z in range(0,len(Matrix_x0)):                    # For each of five organisms

                                                            # Pull values from all arrays at a particular address

            x0 = Matrix_x0[z]
            y0 = Matrix_y0[z]

            theta = Matrix_theta[z]
            a = Matrix_a[z]

            alpha1 = Matrix_alpha1[z]
            alpha2 = Matrix_alpha2[z]


                                                          # Mutate the organism

            if j < 1500:
                delta = 0.001
            else:
                delta = 0.0001

            x0 = x0 + delta*(-1.0+2.0*random.random())
            y0 = y0 + delta*(-1.0+2.0*random.random())

            theta = theta + delta*(-1.0+2.0*random.random())
            a = a + delta*(-1.0+2.0*random.random())

            alpha1 = alpha1 + delta*(-1.0+2.0*random.random())
            alpha2 = alpha2 + delta*(-1.0+2.0*random.random())



                                                        # Evaluate the organism's performance
                                                        # Form a "residual" for each of the six equations
                                                        # Each residual should ideally end up being zero
                                                        # Add the six sub-residuals together to get a total residual
                                                        # The total residual determines the organism's performance

            u1x = math.cos(theta)
            u1y = math.sin(theta)

            u2x = u1y
            u2y = -u1x

            ######################

            resx1 = x0 + alpha1*u1x + a*(alpha1**2.0)*u2x - x1   # Coordinate residuals - four points
            resx2 = x0 + alpha2*u1x + a*(alpha2**2.0)*u2x - x2

            resy1 = y0 + alpha1*u1y + a*(alpha1**2.0)*u2y - y1
            resy2 = y0 + alpha2*u1y + a*(alpha2**2.0)*u2y - y2

            ######################

            A = a*u2y - rt3*a*u2x        # tangency residual #1
            B = u1y - rt3*u1x
            C = y0 - rt3*x0 - 2.0*rt3

            resT1 = B**2.0 - 4.0*A*C

            ######################

            A = a*u2y + 0.5*a*u2x        # tangency residual #2
            B = u1y + 0.5*u1x
            C = y0 + 0.5*x0 + 1.0

            resT2 = B**2.0 - 4.0*A*C

            ######################

            res = 0.0

            res = res + math.fabs(resx1)
            res = res + math.fabs(resx2)
            res = res + math.fabs(resy1)
            res = res + math.fabs(resy2)
            res = res + math.fabs(resT1)
            res = res + math.fabs(resT2)

            residual = res                  # total residual

            Matrix_x0[z] = x0               # store mutated parameters back into organism array
            Matrix_y0[z] = y0

            Matrix_theta[z] = theta
            Matrix_a[z] = a

            Matrix_alpha1[z] = alpha1
            Matrix_alpha2[z] = alpha2


            err_sum_mtrx[z] = residual     # store residual back into corresponding array



                                                        # Find the best organism
                                                        # Best organism has smallest total residual
        best_addr = 99
        secbest_addr = 99

        for z in range(0,len(Matrix_x0)):            # For each organism
            count = 0

            for w in range(0,len(Matrix_x0)):        # Compare with every other organism
                if z != w:                          # Except for itself

                    if err_sum_mtrx[w] < err_sum_mtrx[z]:

                        count = count + 1

            if count == 0:
                best_addr = z

                                                        # Find the second best organism
                                                        # Second best organism has second smallest residual

        for z in range(0,len(Matrix_x0)):                # For each organism
            count = 0

            for w in range(0,len(Matrix_x0)):            # Compare with every other organism
                if (z != w) and (w != best_addr) and (z != best_addr):       # Except for itself and the best organism

                    if err_sum_mtrx[w] < err_sum_mtrx[z]:

                        count = count + 1

            if count == 0:
                secbest_addr = z


                                                    # Breed the two best organisms

        x0_breed_1 = Matrix_x0[best_addr]
        y0_breed_1 = Matrix_y0[best_addr]

        theta_breed_1 = Matrix_theta[best_addr]
        a_breed_1 = Matrix_a[best_addr]

        alpha1_breed_1 = Matrix_alpha1[best_addr]
        alpha2_breed_1 = Matrix_alpha2[best_addr]


        x0_breed_2 = Matrix_x0[secbest_addr]
        y0_breed_2 = Matrix_y0[secbest_addr]

        theta_breed_2 = Matrix_theta[secbest_addr]
        a_breed_2 = Matrix_a[secbest_addr]

        alpha1_breed_2 = Matrix_alpha1[secbest_addr]
        alpha2_breed_2 = Matrix_alpha2[secbest_addr]





        for z in range(0,len(Matrix_x0)):   # For each organism

            # New organism is a randomly weighted average of the two best organisms from the previous generation

            fraction_x0 = random.random()
            fraction_y0 = random.random()

            fraction_theta = random.random()
            fraction_a = random.random()

            fraction_alpha1 = random.random()
            fraction_alpha2 = random.random()


            Matrix_x0[z] = fraction_x0 * x0_breed_1 + (1.0 - fraction_x0) * x0_breed_2
            Matrix_y0[z] = fraction_y0 * y0_breed_1 + (1.0 - fraction_y0) * y0_breed_2

            Matrix_theta[z] = fraction_theta * theta_breed_1 + (1.0 - fraction_theta) * theta_breed_2
            Matrix_a[z] = fraction_a * a_breed_1 + (1.0 - fraction_a) * a_breed_2

            Matrix_alpha1[z] = fraction_alpha1 * alpha1_breed_1 + (1.0 - fraction_alpha1) * alpha1_breed_2
            Matrix_alpha2[z] = fraction_alpha2 * alpha2_breed_1 + (1.0 - fraction_alpha2) * alpha2_breed_2



#####################################################################################################
#####################################################################################################

# One final evaluation outside of the main loop

for z in range(0,len(Matrix_x0)):                    # For each of five organisms

    x0 = Matrix_x0[z]
    y0 = Matrix_y0[z]

    theta = Matrix_theta[z]
    a = Matrix_a[z]

    alpha1 = Matrix_alpha1[z]
    alpha2 = Matrix_alpha2[z]



                                                # Evaluate the organism performance

    u1x = math.cos(theta)
    u1y = math.sin(theta)

    u2x = u1y
    u2y = -u1x

    ######################

    resx1 = x0 + alpha1*u1x + a*(alpha1**2.0)*u2x - x1
    resx2 = x0 + alpha2*u1x + a*(alpha2**2.0)*u2x - x2

    resy1 = y0 + alpha1*u1y + a*(alpha1**2.0)*u2y - y1
    resy2 = y0 + alpha2*u1y + a*(alpha2**2.0)*u2y - y2

    ######################

    A = a*u2y - rt3*a*u2x
    B = u1y - rt3*u1x
    C = y0 - rt3*x0 - 2.0*rt3

    resT1 = B**2.0 - 4.0*A*C

    ######################

    A = a*u2y + 0.5*a*u2x
    B = u1y + 0.5*u1x
    C = y0 + 0.5*x0 + 1.0

    resT2 = B**2.0 - 4.0*A*C

    ######################

    res = 0.0

    res = res + math.fabs(resx1)
    res = res + math.fabs(resx2)
    res = res + math.fabs(resy1)
    res = res + math.fabs(resy2)
    res = res + math.fabs(resT1)
    res = res + math.fabs(resT2)

    residual = res

    err_sum_mtrx[z] = residual

####################################################################################################

                                                # Find the best organism
best_addr = 99
secbest_addr = 99

for z in range(0,len(Matrix_x0)):            # For each organism
    count = 0

    for w in range(0,len(Matrix_x0)):        # Compare with every other organism
        if z != w:                          # Except for itself

            if err_sum_mtrx[w] < err_sum_mtrx[z]:

                count = count + 1

    if count == 0:
        best_addr = z


####################################################################################################

# Parameters for the overall final result

x0 = Matrix_x0[best_addr]
y0 = Matrix_y0[best_addr]

theta = Matrix_theta[best_addr]
a = Matrix_a[best_addr]

alpha1 = Matrix_alpha1[best_addr]
alpha2 = Matrix_alpha2[best_addr]

err_sum = err_sum_mtrx[best_addr]

####################################################################################################
####################################################################################################

# Print results

print ""
print "###################################"
print ""

print "Outputs"

sys.stdout.write("errsum = ")
print(err_sum)
print ""

sys.stdout.write("x0 = ")
print(x0)
print ""

sys.stdout.write("y0 = ")
print(y0)
print ""

sys.stdout.write("theta = ")
print(180.0 * theta / math.pi)
print ""

sys.stdout.write("a = ")
print(a)
print ""

sys.stdout.write("alpha1 = ")
print(alpha1)
print ""

sys.stdout.write("alpha2 = ")
print(alpha2)
print ""

sys.stdout.write("f = ")
print(1.0/(4.0*a))
print ""



print ""
print "###################################"
print ""

0 Helpful 0 Interesting 2 Brilliant 0 Confused

Wow, fantastic solution. Would you mind posting your code? The GA sounds interesting.

Chris Lewis - 1 year, 11 months ago

Log in to reply

I have added the code to the end of the solution. I programmed the structure of the GA program several years ago, and modified it for this particular application.

Steven Chase - 1 year, 11 months ago

Also, I made the mutation size dynamic, which yielded better convergence. The new results are posted too

Steven Chase - 1 year, 11 months ago

Log in to reply

Awesome, thank you!

Chris Lewis - 1 year, 11 months ago

Thanks. Sure, I'll post it this evening.

Steven Chase - 1 year, 11 months ago

Iliya Hristov - 1 year, 1 month ago

It is possible to find an exact solution, but the expression is very long.

Iliya Hristov - 6 months, 2 weeks ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...