Let's go back a couple years
∫ − π / 2 π / 2 2 0 0 7 x + 1 1 ⋅ sin 2 0 0 8 x + cos 2 0 0 8 x sin 2 0 0 8 x d x = ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
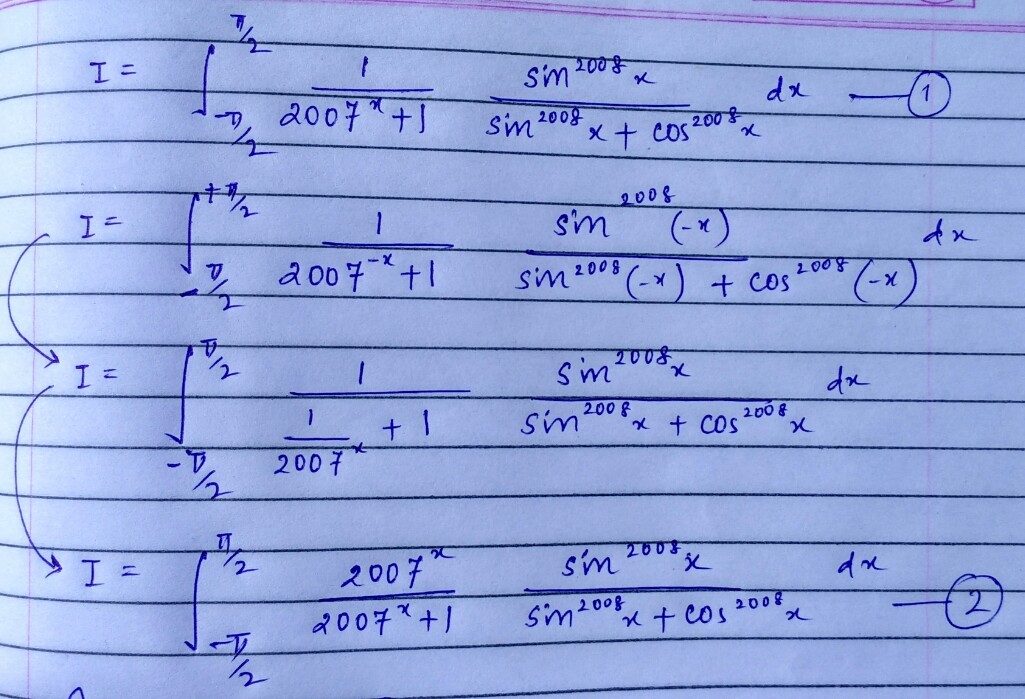

When did you learn these? (I am a math enthusiast from class 10!)
Log in to reply
I learnt integration in class 12 CBSE :)
Where are you take such questions?
Log in to reply
I am not able to understand your question, please elaborate :)
I = ∫ − 2 π 2 π 2 0 0 7 x + 1 1 ⋅ sin 2 0 0 8 x + cos 2 0 0 8 x sin 2 0 0 8 x d x = ∫ − 2 π 0 2 0 0 7 x + 1 1 ⋅ sin 2 0 0 8 x + cos 2 0 0 8 x sin 2 0 0 8 x d x + ∫ 0 2 π 2 0 0 7 x + 1 1 ⋅ sin 2 0 0 8 x + cos 2 0 0 8 x sin 2 0 0 8 x d x = ∫ 0 2 π 2 0 0 7 − x + 1 1 ⋅ sin 2 0 0 8 x + cos 2 0 0 8 x sin 2 0 0 8 x d x + ∫ 0 2 π 2 0 0 7 x + 1 1 ⋅ sin 2 0 0 8 x + cos 2 0 0 8 x sin 2 0 0 8 x d x = ∫ 0 2 π 1 + 2 0 0 7 x 2 0 0 7 x ⋅ sin 2 0 0 8 x + cos 2 0 0 8 x sin 2 0 0 8 x d x + ∫ 0 2 π 2 0 0 7 x + 1 1 ⋅ sin 2 0 0 8 x + cos 2 0 0 8 x sin 2 0 0 8 x d x Replace x with − x
= ∫ 0 2 π sin 2 0 0 8 x + cos 2 0 0 8 x sin 2 0 0 8 x d x = 2 1 ∫ 0 2 π ( sin 2 0 0 8 x + cos 2 0 0 8 x sin 2 0 0 8 x + cos 2 0 0 8 x + sin 2 0 0 8 x cos 2 0 0 8 x ) d x = 2 1 ∫ 0 2 π d x = 4 π Using ∫ a b f ( x ) d x = ∫ a b f ( a + b − x ) d x