Let's Go Outside
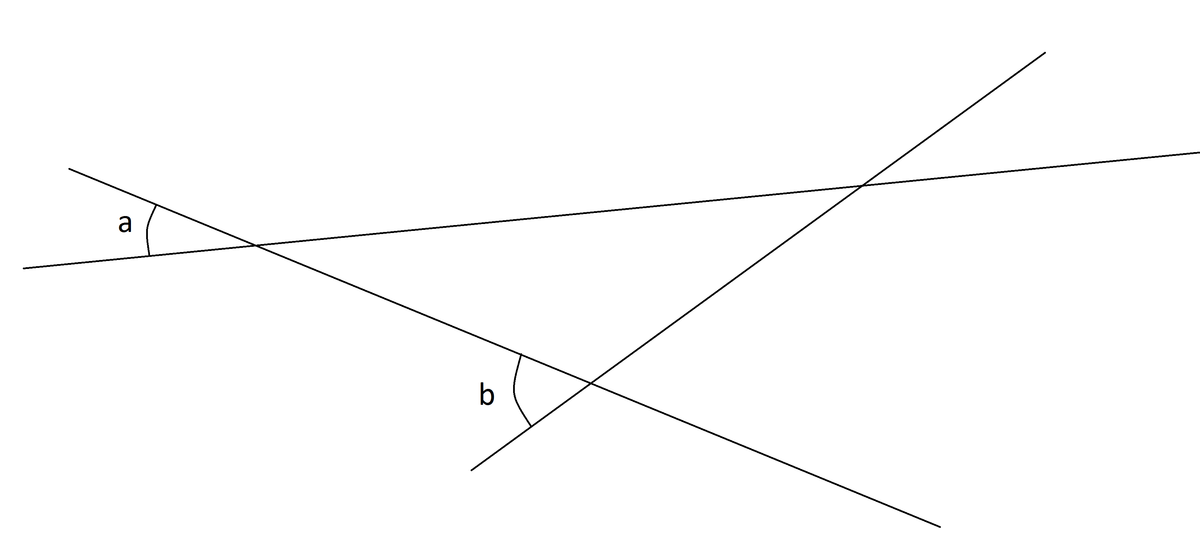
There exist four circles which are each tangent to all three lines in the figure above. One of those circles is inside the triangle defined by these lines. (We are not interested in that one.) The centers of the remaining three form a triangle. Given and , what is the angle of this triangle at the vertex directly opposite angle ?
The answer is 64.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The triangle defined by the three lines has internal angles as listed in red in the figure above. The center of the circle is located at an intersection of angle bisectors, so two of the angles in blue can each be obtained as a half of 180 minus the relevant inside angle. The 64 is then just what's left of 180 inside a triangle.
(Or you can do the calculation in one step, as an average of 105 and 23.)