Lets have a straight talk!
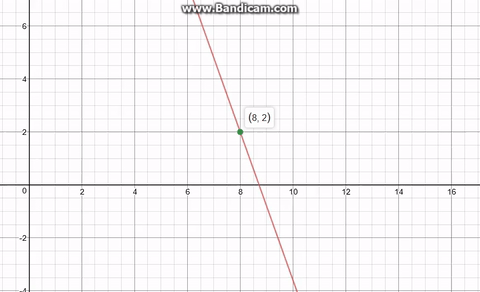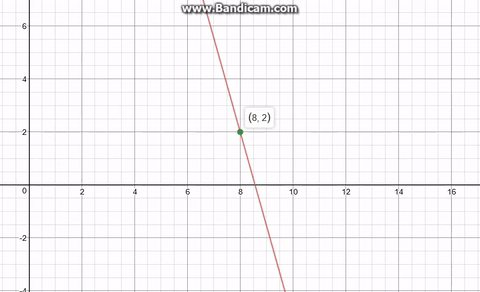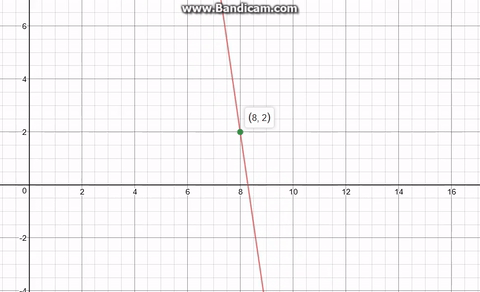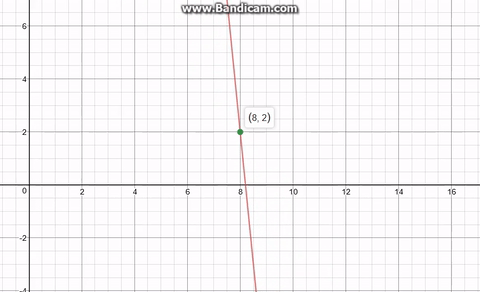 A straight line
L
with negative slope passes through the point
(
8
,
2
)
and cuts the positive coordinate axes at points
P
and
Q
. Find the the absolute minimum value of
O
P
+
O
Q
, as
L
varies where
O
is the origin.
A straight line
L
with negative slope passes through the point
(
8
,
2
)
and cuts the positive coordinate axes at points
P
and
Q
. Find the the absolute minimum value of
O
P
+
O
Q
, as
L
varies where
O
is the origin.
This is a part of the set JEE Fest .
The answer is 18.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Let m ∈ R + be the slope of line L in question, which is represented as y − 2 = − m ( x − 8 ) ⇒ y = − m x + ( 8 m + 2 ) . The corresponding y and x-intercepts, P and Q , are given as:
P ( 0 , 8 m + 2 ) ; Q ( 8 + m 2 , 0 )
and O P + O Q = L ( m ) = ( 8 m + 2 ) + ( 8 + m 2 ) = 1 0 + 8 m + m 2 . as a function of the slope m . Differentiating L ( m ) produces:
L ′ ( m ) = 8 − m 2 2 = 0 ⇒ 8 m 2 = 2 ⇒ m = 2 1 (since we require m > 0 ) .
and L ′ ′ ( m ) = m 3 4 ⇒ L ′ ′ ( 2 1 ) > 0 (hence, a minimum).
Thus, the minimum value of O P + O Q is L ( 2 1 ) = 1 0 + 8 ( 2 1 ) + 2 1 2 = 1 8 .

Similar solution with @Dheeman Kuaner 's
Suppose that line L cuts the x - and y -axis at P and Q respectively. Let O P = a , O Q = b and ∠ Q P O = θ . Then we have:
⎩ ⎪ ⎨ ⎪ ⎧ tan θ = a − 8 2 tan θ = a b ⟹ a = tan θ 2 + 8 ⟹ b = a tan θ = 2 + 8 tan θ
Then we have: O P + O Q = a + b = tan θ 2 + 1 0 + 8 tan θ . Using AM-GM inequality tan θ 2 + 8 tan θ ≥ 2 1 6 = 8 . Therefore O P + O Q ≥ 1 8