Let's make the signs alternate

Let $A = 1 + \frac{1}{4} + \frac{ 1}{16} + \ldots$ and
let $B = \frac{1}{2} + \frac{ 1}{8} + \frac{1}{32} + \ldots$ .

We see that $2B = A$ . The question asks:

$A + B = \text{\_\_} ( A - B)$

Substituting in $B = \frac{A}{2}$ , we get $\frac{3}{2} A = \text{\_\_} ( \frac{1}{2} A)$ .

Hence, the answer is 3.

Note: What assumption does this solution make?

Using the formula for a sum of geometric series $S=\frac a{1-r}$ with $a=1$ and $r=\frac12$ on the left and $a=1$ and $r=-\frac12$ on the right.

$\dfrac1{1-\frac12}=x\times\dfrac1{1+\frac12}$

$2=\frac23x$

$x=\boxed3$

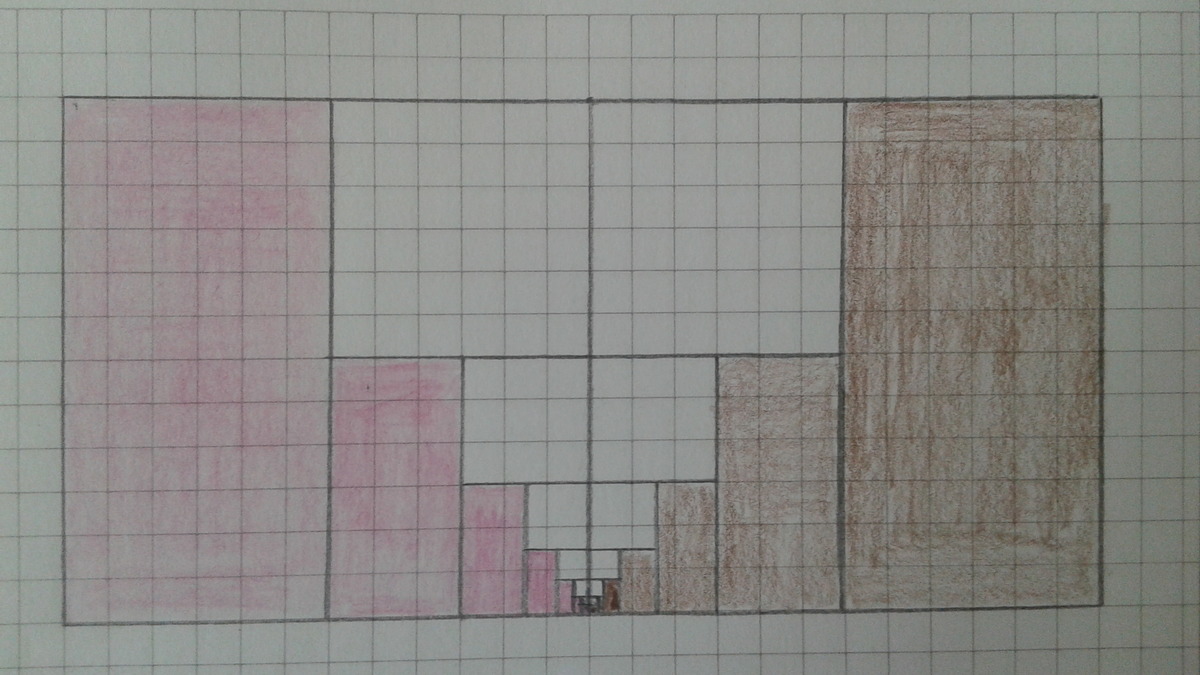
The sum of the Progression of $\frac{1}{2^n}$ is equal to two. I visualized this with two squares. The second sum diverges to $\frac{2}{3}$ . The convergence is simple to proof when you set brackets. (1- $\frac{1}{2}$ ) + ( $\frac{1}{4}$ - $\frac{1}{8}$ ) + ... is equal to the sum of $\frac{1}{2^{2*n-1}}$ for n > 0.

This series converges to $\frac{2}{3}$ , since the difference between the sum is always for $\frac{1}{2^{2*n-1}}$ equal to $\frac{1}{(2^{2*n-1}*3)}$ . $\frac{2}{3}$ * 3 = 2

You can see, that the alternate series is $\frac{1}{3}$ of the geometric series good in the visualization, I choosed for this.

Reorganize the sequence

Left side:

= (1+ $\frac{1}{2}$ ) + ( $\frac{1}{4}$ + $\frac{1}{8}$ ) + ( $\frac{1}{16}$ + $\frac{1}{32}$ ) + ...

= $\frac{3}{2}$ + $\frac{3}{8}$ + $\frac{3}{16}$ + ...

Right side:

= (1- $\frac{1}{2}$ ) + ( $\frac{1}{4}$ - $\frac{1}{8}$ ) + ( $\frac{1}{16}$ - $\frac{1}{32}$ ) + ...

= $\frac{1}{2}$ + $\frac{1}{8}$ + $\frac{1}{16}$ + ...

Hence, the answer is 3.

Since the given series $\sum_{n = 0}^{\infty} (-1)^n \dfrac{1}{2^n}$ converges absolutely we can rearrange the terms so that:

$\sum_{n = 0}^{\infty} \dfrac{1}{4^n} = \dfrac{4}{3}$

and,

$-\dfrac{1}{2} \sum_{n = 0}^{\infty} \dfrac{1}{4^n} = -\dfrac{2}{3}$

$\implies \sum_{n = 0}^{\infty} (-1)^n \dfrac{1}{2^n} = \dfrac{2}{3}$

and $\sum_{n = 0}^{\infty} \dfrac{1}{2^n} = 2 \implies 2 = \dfrac{2}{3} j \implies j = 3.$

An alternative way to tackle this question is by finding the limits of the geometric series. These series are famous enough that some may know them by heart, but here is the method:

The sum of the first $n$ terms with first term $a$ and common ratio $r \neq 1$ is:

$S_n=\frac {a(1-r^n)}{1-r}$

Now we take the limit as $n \rightarrow \infty$

Provided that $-1 \leq r < 1$ , the limit simplifies to $\frac {a}{1-r}$

Now we simply substitute

The LHS: $\frac {(1)}{1-(1/2)}=2$

The RHS series: $\frac {(1)}{1-(-1/2)}=2/3$

The missing value is $x=\frac {2}{2/3}=3$

${\color{#3D99F6}1} + {\color{#D61F06}\dfrac12} + {\color{#3D99F6}\dfrac14} + {\color{#D61F06}\dfrac18} +{\color{#3D99F6}\dfrac1{16}} + \cdots = \text{\_\_\_\_\_\_\_} \times \left({\color{#3D99F6}1} - {\color{#D61F06}\dfrac12} + {\color{#3D99F6}\dfrac14} - {\color{#D61F06}\dfrac18} + {\color{#3D99F6}\dfrac1{16}} - \cdots \right)$

Let sum of G.P in L.H.S. = S1,

sum of G.P. in R.H.S. = S2

and blank space that we have to find be A

S1 = $\frac{a}{1-r}$ = $\frac{1}{1-(\frac{1}{2})}$ = 2

S2 = $\frac{a}{1-r}$ = $\frac{1}{1-(\frac{-1}{2})}$ = $\frac{2}{3}$

S1 = A * S2

A = $\frac{S1}{S2}$

= $\frac{2}{(\frac{2}{3})}$

A = 3

Considering the terms in pairs we see that each partial sum of the positive term series, taken in pairs, is three times the partial sum of the corresponding pairs of the alternating term series. Since we know that both series converge this is sufficient to get the answer 3.

That is, since

$\sum_{k=0}^{2n-1} 2^{-k} = 3 \sum_{k=0}^{2n-1} (-1)^k2^{-k}$ for all n > 0 and both series converge (sum of remaining terms can be made arbitrarily small) we can conclude that

$\sum_{k=0}^{\infty} 2^{-k} = 3 \sum_{k=0}^{\infty} (-1)^k2^{-k}$

This approach is very similar to the approximation solution to 100 Day Summer Challenge Day 58 with nested squares instead of missing corners as in this problem. The ultimate fraction becomes apparent early on in a structural way in both.

One might also notice that both are geometric series that can be computed directly via $\frac {1} {1-r}$ with r = $\frac{1}{2}$ and r = $\frac{-1}{2}$ respectively to get 2 and 2/3 for sums and the answer 3.