Let's meet at a point
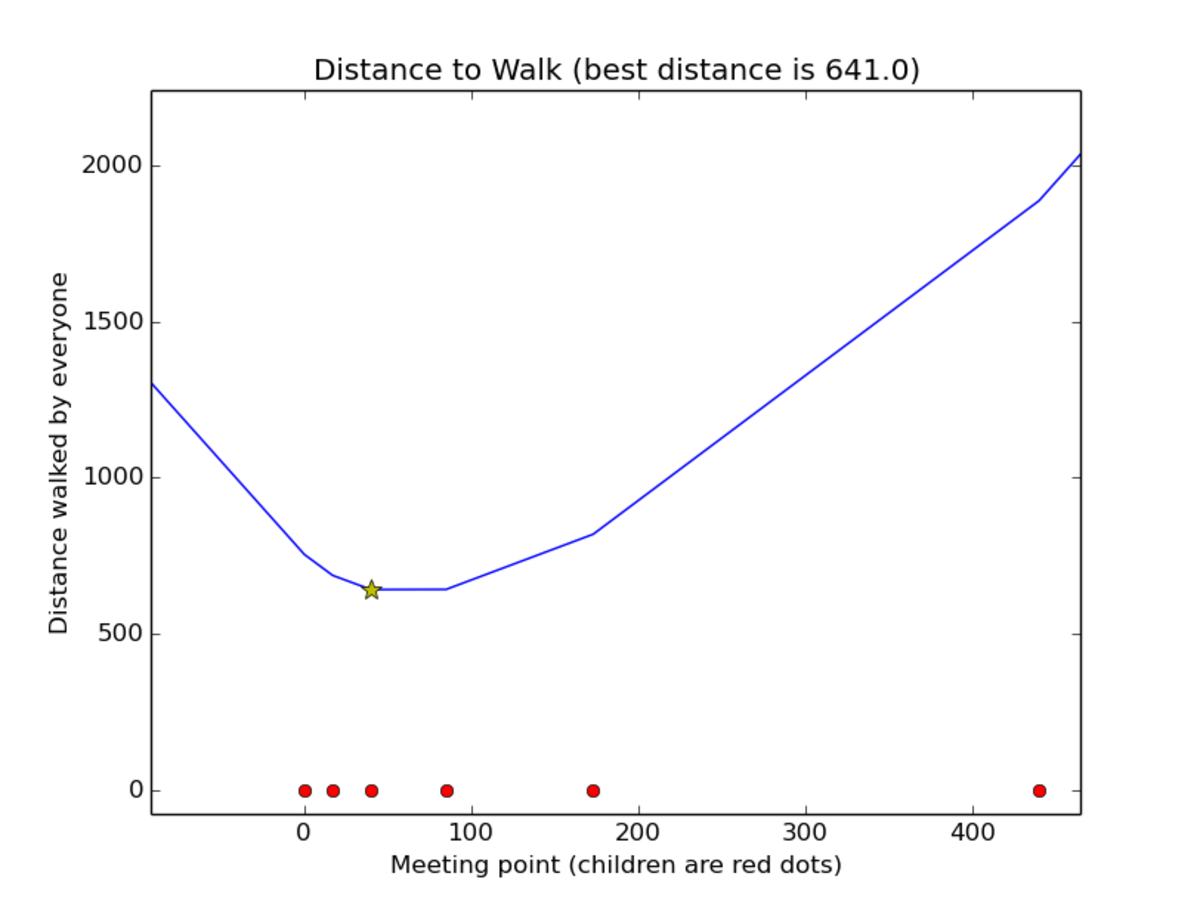
Six children are standing along the x -axis at points ( 0 , 0 ) , ( 1 7 , 0 ) , ( 4 0 , 0 ) , ( 8 5 , 0 ) , ( 1 7 3 , 0 ) , ( 4 4 0 , 0 ) . The children decide to meet at some point along the x -axis. What is the minimum total distance the children must walk in order to meet?
The answer is 641.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
16 solutions
Most solutions did a tedious case by case analysis, and did not consider how they can simplify their explanations. These are 2 straightforward arguments that give the result almost immediately.
Why the reversal in the fifth and sixth term? How do you justify that without a case-by-case analysis?
Log in to reply
The last three terms are flipped so that the a's cancel out, not for any geometric reason. |a-85|=|85-a| regardless of which is bigger.
I see nothing wrong with Sameer Kailasa's explanation; but if you're looking for another proof that case-by-case analysis is unnecessary, consider this: the nth child (noting the fact that they're in order left-to-right) and the (7-n)th child must travel a combined total of at least the distance between them, and that minimum is achievable if and only if the meeting point lies in between them. The rest follows easily.
This does give a lower bound on the answer, but I think you need to provide an example where 641 is achieved.
If you had to chose a point that minimizes the distance from two other points it is quite clear you would have to chose one between these two points. Also: the distance would be the same for any point between these two. Now view the problem with this same technique:
View the sum of 6 distances as the sum of 3 pairs of distances (paring up the greatest with the smallest, the second greatest with the second smallest and so on.) Then it is clear that to minimizethe sum you need to pick a point in the middle of all of these pairs ( in other words: between (40,0) and (85,0). Choose any of these points and find the sum of the distances.
I did the same
There are only 3 cases we can consider in the question.Let ( x , 0 ) be the place where they meet.
Case 1:
Let x be 1 7 3 ≤ x ≤ 4 4 0
So the total distance for the 6 children to go to ( x , 0 ) is ( 4 4 0 − x ) + ( x − 1 7 3 ) + ( x − 8 5 ) + ( x − 4 0 ) + ( x − 1 7 ) + x , which is 4 x + 1 2 5
Before jumping into any conclusion, let's see the second case first.
Case 2:
Let x be 8 5 ≤ x < 1 7 3
The total distance for the 6 children to go to ( x , 0 ) is ( 4 4 0 − x ) + ( 1 7 3 − x ) + ( x − 8 5 ) + ( x − 4 0 ) + ( x − 1 7 ) + x , which is 2 x + 4 7 1
Again, we observe the third case before deciding the conclusion.
Case 3:
Let x be 4 0 ≤ x < 8 5
The total distance for the 6 children to go to ( x , 0 ) is ( 4 4 0 − x ) + ( 1 7 3 − x ) + ( 8 5 − x ) + ( x − 4 0 ) + ( x − 1 7 ) + x , which is 641, a constant.
Now we can consider and observe every case.
Case 1: 4 x + 1 2 5 , where x is 1 7 3 ≤ x ≤ 4 4 0
Case 2: 2 x + 4 7 1 , where x is 8 5 ≤ x < 1 7 3
Case 3: 6 4 1 , where x is 4 0 ≤ x < 8 5
To make the values as small as possible, we take x as 173 for Case 1, 85 for Case 2. For Case 3, there is nothing to do as we no longer have a variable, we just have a constant.
Now we can clearly see the results.
Case 1: 817
Case 2: 641
Case 3: 641
Clearly, the minimum total distance for all cases when the children walk in order to meet is 641.
Note: We just test cases where x is 1 7 3 ≤ x ≤ 4 4 0 , 8 5 ≤ x < 1 7 3 and 4 0 ≤ x < 8 5 because the other cases are clearly out. For example: When x is > 4 4 0 , they must all walk towards a point, which is not the minimum distance. For x is 1 7 ≤ x < 4 0 and 0 ≤ x < 1 7 , the meeting points are to far from 440, which makes the total distance even larger.
Solution 1: Clearly the children shouldn't walk in the y-direction at all. Suppose the children meet at the point P = ( n , 0 ) . If there are more children to the right of P than there are to the left of P , we can let P = ( n + 1 , 0 ) and decrease the total distance travelled. Similarly, if there are more children to the left of P , then we could let P = ( n − 1 , 0 ) and decrease the total distance. Thus, the meeting point should be between ( 4 0 , 0 ) and ( 8 5 , 0 ) . For any point in this interval, the total distance travelled by the first and last child is 4 4 0 − 0 = 4 4 0 , the total travelled by the second and fifth child is 1 7 3 − 1 7 = 1 5 6 and the total travelled by the third and fourth is 8 5 − 4 0 = 4 5 . Thus, the minimum total distance is 4 4 0 + 1 5 6 + 4 5 = 6 4 1 .
Solution 2: If the children were to meet at point ( x , 0 ) , then the total distance that they walk is f ( x ) = ∣ x − 0 ∣ + ∣ x − 1 7 ∣ + ∣ x − 4 0 ∣ + ∣ x − 8 5 ∣ + ∣ x − 1 7 3 ∣ + ∣ x − 4 4 0 ∣ . We know that the minimum of this graph occurs at one of the kinked points, so we test the values of f ( 0 ) , f ( 1 7 ) , f ( 4 0 ) , f ( 8 5 ) , f ( 1 7 3 ) , f ( 4 4 0 ) , and see that it achieves a minimum of 641 at f ( 4 0 ) and f ( 8 5 ) .
Shouldn't the solution of x that minimize f ( x ) be x ∈ [ 4 0 , 8 5 ] ? Not only x = 4 0 and x = 8 5 ???
It's pretty obvious that their meeting place won't be outside the range [ 0 , 4 4 0 ] , since that is less efficient than going to either 0 or 440. There are five cases to consider for x's location: ( 0 , 1 7 ) , ( 1 7 , 4 0 ) , ( 4 0 , 8 5 ) , ( 8 5 , 1 7 3 ) , and ( 1 7 3 , 4 4 0 ) . ( 0 , 1 7 ) is relatively improbable, so I will leave that for last.
For the domain x is part of ( 4 0 , 8 5 ) , the expression for the total distance walked will be (x)+(x-17)+(x-40)+(85-x)+(173-x)+(440-x), which simplifies to 755.
For the domain x is part of ( 8 5 , 1 7 3 ) , the expression for the total distance walked will be (x)+(x-17)+(x-40)+(x-85)+(173-x)+(440-x), which simplifies to 2x+471. In order to minimize that, we choose the smallest possible value for x, which is 85. Plugging that in, the distance walked in this case is 641.
For the domain x is part of ( 1 7 3 , 4 4 0 ) , the expression for the total distance walked will be (x)+(x-17)+(x-40)+(85-x)+(x-173)+(440-x), which simplifies to 4x+125. At a glance, 4x is greater than 170*4-680, making this option not posssible.
Since 641 is less than 755, 6 4 1 is the answer.
For the domain x is part of (40,85), it simplifies to 85+173+440-40-17=641 (instead of 755).
Child 1 and Child 6 together must walk a total of 440 to meet somewhere between their starting points. If they meet elsewhere they will have to walk further.
The same argument applies to Child 2 and 5, but with a total of 173 - 17 = 156, and to Child 3 and 4 with 85 - 40 = 45.
440 + 146 + 45 = 641.
My solution that suddenly came out of instinct: We can combine the minimum total distance that must be travelled by this pairs of students, marked by their x-axis position: (0,440), (17,173), (40,85). by this we simply get 440+173+85-40-17-0=641.
We have to find the minimum possible total distance walked by the 6-children ,mentioned above, to meet at a same point... suppose if that point is between 1st and 2nd children than one child has to come forward and the other five has to come backward but the number of children coming forward should be equal to the number of children coming backward so, that point should be in between 3rd and 4th child..... hence any point between 3rd and 4th child can be the point for which the total distance is minimum... also amazingly the points at which the 3rd and 4th child are standing can also be that required point.. in this case and given conditions the total distance will be 641.
Trial and error shows that anything between 40 and 80 sums up to 641.
let x be the distance from origin where all children are going to meet each other. distance travelled by a children at (0,0)=x " " " " " " " " " " " (17,0)=x-17 " " " " " " " " " " " (40,0)=x-40 for the distance travelled by them ,x should lie between (40,0) &(85,0), distance travelled by a children at(85,0)=85-x distance travelled by a children at(173,0)=173-x distance travelled by a children at (440,0)=440-x adding all these we get the answer
Note that the solution 641 is achieved when the location is between the two middle values of the range of locations. If there were an odd number of children then the minimum distance would occur at the location of the middle child, i.e, the median location.
Let us deliberately start with a 'bad' value of meeting point M and start optimizing.
Start with M at x = 0. Then the total walk is simply the sum of the six coordinates. And the child at x = 0 doesn't walk at all.
Now move M to x = 1. The child at x = 0 walks 1 unit more than before. But the rest of the five kids walk 1 unit less each. Saving 4 units of walking!
So optimization has to do with how many stand on either side. If M is chosen to place three kids on both sides, the total loss will compensate the total gain and no more optimization is possible. So it is already optimized!
Hence M must lie between x = 40 and x = 85, For ease of calculation take any one of these values and calculate getting 641
Let (a,0) be the meeting point. Then the total distance can be expressed as a function of a, let's call it D(a). D ( a ) = ∣ a ∣ + ∣ a − 1 7 ∣ + ∣ a − 4 0 ∣ + ∣ a − 8 5 ∣ + ∣ a − 1 7 3 ∣ + ∣ a − 4 4 0 ∣ There may be a min at D'(a) = 0.
D ′ ( a ) = a ∣ a ∣ + a − 1 7 ∣ a − 1 7 ∣ + a − 4 0 ∣ a − 4 0 ∣ + a − 8 5 ∣ a − 8 5 ∣ + a − 1 7 3 ∣ a − 1 7 3 ∣ + a − 4 4 0 ∣ a − 4 4 0 ∣
Each of these terms is either 1 or -1 so, for the sum to be zero, then 3 must be 1 and the other 3 must be -1, i.e. a must be between 40 and 85. So, D(a) can be rewritten without the absolute value symbols as: D ( a ) = a + ( a − 1 7 ) + ( a − 4 0 ) + ( 8 5 − a ) + ( 1 7 3 − a ) + ( 4 4 0 − a ) = 6 4 1
Note I omitted the second derivative test out of pure laziness but the stationary point has to be a minimum in this case so I think I'm okay :)
Suppose we have 2 n points a 1 < … < a 2 n in the real line, and we want to minimize the sum of distances to a point. Then we want to minimize the function f ( x ) = i = 1 ∑ 2 n ∣ x − a i ∣ . This function is convex as a sum of convex functions, and it is constant on the central segment [ a n , a n + 1 ] because moving x in that segment implies adding a constant to each of the n summands ∣ x − a 1 ∣ , … , ∣ x − a n ∣ and substracting the same constant to each of the n summands ∣ x − a n + 1 ∣ , … , ∣ x − a 2 n ∣ . Then any point lying in (the interior of) the segment [ a n , a n + 1 ] is a local minimum of f ( x ) , and hence a global minimum since f ( x ) is convex. We deduce that the minimum value is f ( a n ) .
In our case, the minimum is f ( 4 0 ) = ∣ 4 0 − 0 ∣ + ∣ 4 0 − 1 7 ∣ + ∣ 4 0 − 4 0 ∣ + ∣ 8 5 − 4 0 ∣ + ∣ 1 7 3 − 4 0 ∣ + ∣ 4 0 − 4 4 0 ∣ = 6 4 1 .
Python 3.4:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
|
Dependencies:
-
matplotlib (
sudo apt-get install python3-matplotlib)
for the minimum total distance all the children should walk to meet,they all should go to the point (85,0) as it is very closer to all when compared to other numbers.so the total minimum distance = (85-0) + (85-17) +(85-40) + (173-85) + (440-85) = 85 +68 + 45 + 88 +355 =641
Intuitively, if we have a set of numbers x 1 , x 2 , ⋯ , x n , then the inequality ∣ x 1 ∣ + ∣ x 2 ∣ + ⋯ ∣ x n ∣ ≥ ∣ x 1 + x 2 + ⋯ x n ∣ is always true since the every number is individually "turned positive" on the left hand side while some numbers can "cancel" on the right hand side. This is formally known as the triangle inequality.
Coming back to our original problem, we can let the point on the x -axis where the total distance is minimized be ( a , 0 ) . Then the total distance is ∣ a ∣ + ∣ a − 1 7 ∣ + ∣ a − 4 0 ∣ + ∣ 8 5 − a ∣ + ∣ 1 7 3 − a ∣ + ∣ 4 4 0 − a ∣ . By the triangle inequality, the minimum of this value is ∣ a + a − 1 7 + a − 4 0 + 8 5 − a + 1 7 3 − a + 4 4 0 − a ∣ = ∣ 6 4 1 ∣ = 6 4 1 .