Let's Minimize
Number Theory
Level
3
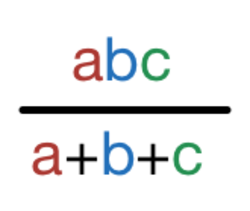Find the
-digit number such that the ratio of this number to the sum of its digits, is minimum.
The answer is 199.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Let the 3-digit number be 100x+10y+z where x, yand z are the hundredth, tenth and ones digit respectively.
We have to minimize the ratio :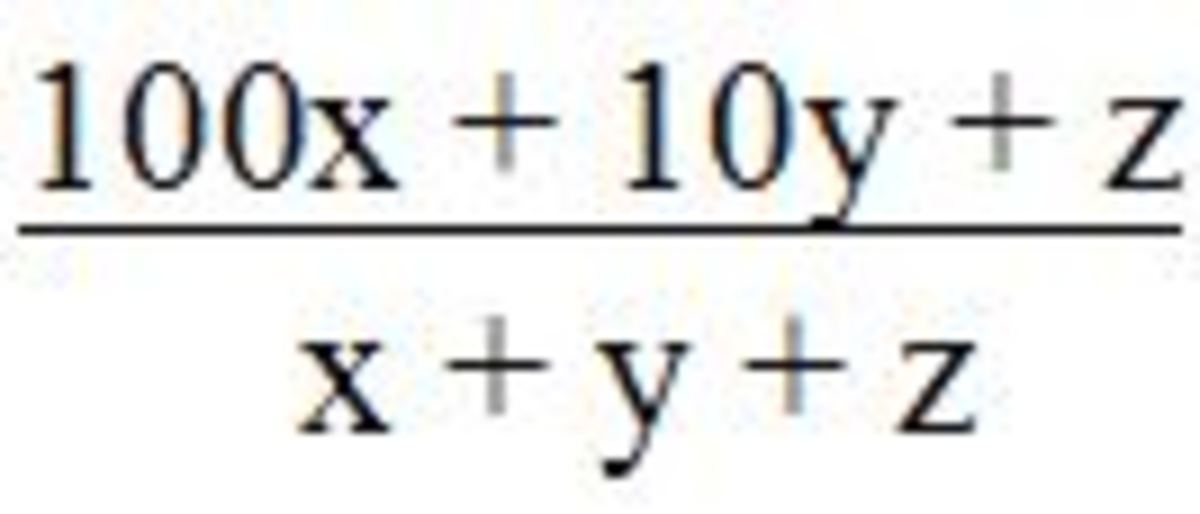
It can be simplified to :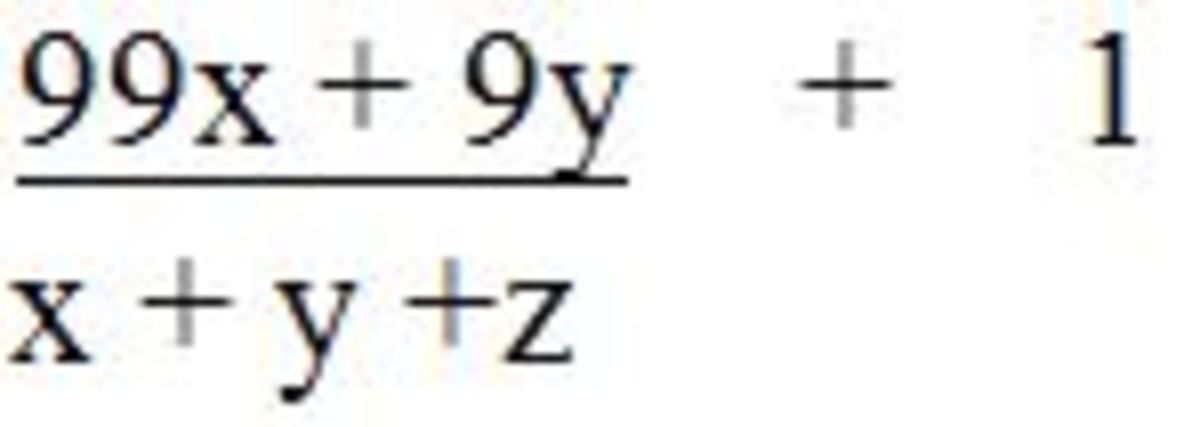
For the above ratio to be minimum, we have to simultaneously minimize 99x + 9y and maximize x+y+z. So z has to be 9 (largest digit) to make the sum of x+y+z as maximum. For x and y, we have to consider both numerator and denominator. Since x is multiplied by 99 in the numerator so x has a more dominant effect on numerator than denominator. So x should be minimum so as to make 99x minimum. So x has to be 1 (x can't be 0 as it is the hundredth digit of a 3-digit number). So the number is of the form 1y9. Try all the 10 possibilities i.e. 109,119,129,..........., 199. The minimum ratio is found if the number is 199.