Let's play!
In a game, named "Let's play", there are two players: Anna and Joe. Anna starts the game. They alternately choose a number from -4, -3, -2, -1, 0, 1, 2, 3, 4. The one who first chooses three numbers, the amount of which is exactly 0, wins the game. Does anybody have a winner strategy? (By winner strategy I mean a strategy with which we can always win.)
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
We will use that there is no winner strategy in a 3 × 3 tic-tac-toe. We can put the -4, -3, -2, -1, 0, 1, 2, 3, 4 numbers into a 3 × 3 square so that if three numbers' amount is 0, then they are in the same row/column/diagonal.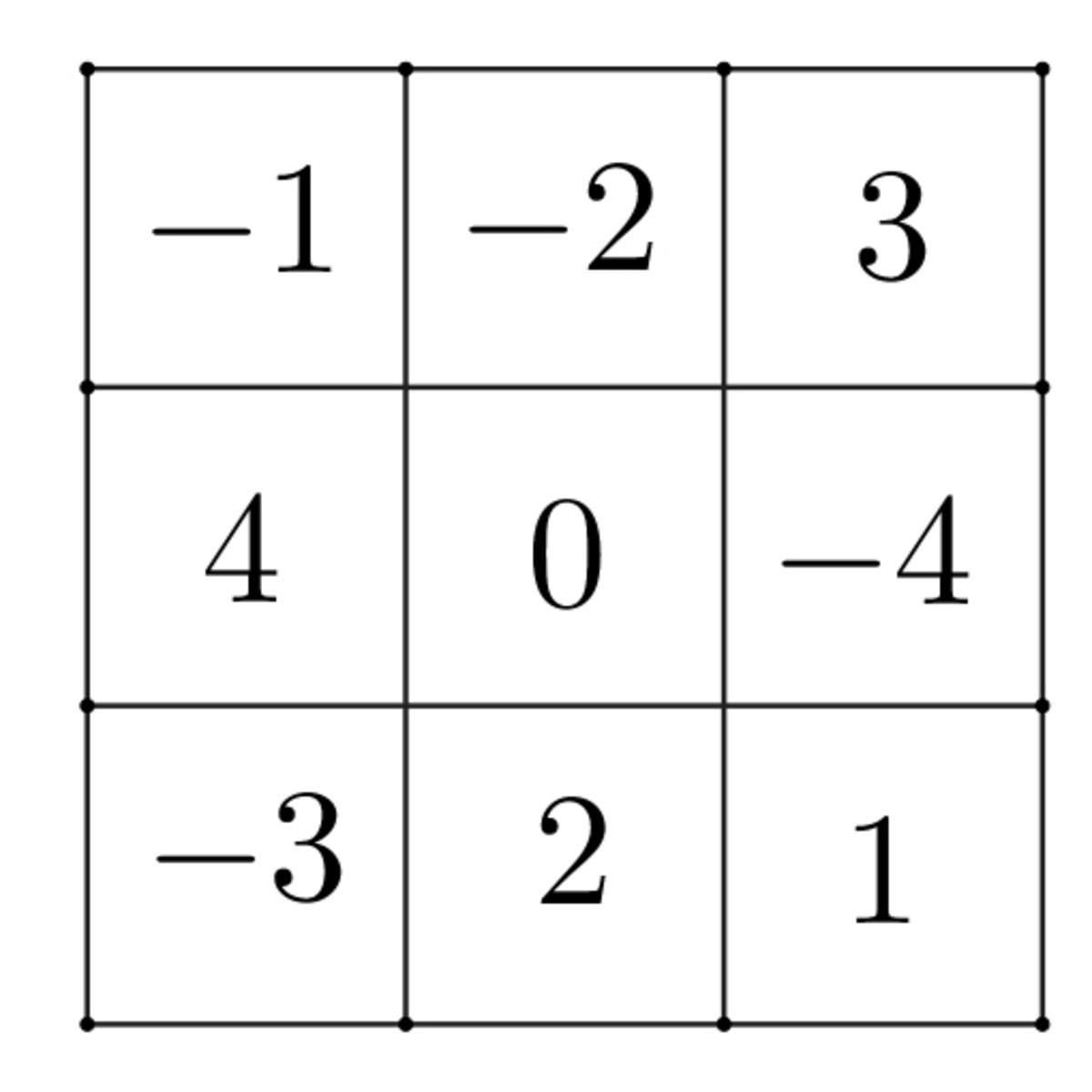
So there's no winner strategy.