Let's play carrom

Geometry Level 5

Me and my sister are playing carrom one evening. Since I am a maths student, I try to implement it into carrom as well, I play a quite neat shot that pushes the carrom coin neatly into the hole but not after having some collisions with the board.

The mathematics of the situation is as follows :

Imagine the boundaries of the carrom board to be the line segements $xy(x-1)(y-1)=0 , 0 \le x,y \le1$ and the holes to be the points $(0,0) , (1,0) , (0,1) , (1,1)$

A carrom coin is pushed from the point $\left (\dfrac{1}{2} , 0 \right )$ with a non-zero velocity. Such that it collides with the carrom board firstly at the point $\left ( \dfrac{2}{15} , 1 \right )$ with the carrom board. Find the total number of collisions the coin makes with the carrom board before going into any of the hole.

Details and Assumptions

1)The size of coin and the hole are negligible, that is they are very small(and the size of the hole is just greater than that of coin. That for the coin to go into the hole it must go exactly into the hole. No near cases must be considered)

2) There is no friction on the carrom board. Hence the coin must go on and on, till it reaches the hole. Also while calculating total number of collisions count the first collision too( that is collision at the point $\left (\dfrac{2}{15},1 \right )$

3) The collisions the coin makes with the carrom board are elastic that is angle of incidence is equal to angle of reflection.

This is original.

Image credit: Wikipedia Bernard Gagnon

The answer is 19.

1 solution

Mvs Saketh
Mar 3, 2015

Such a beautiful problem, here is my way

Suppose That the coin strikes a vertical wall, (Refer to figure for what i mean by vertical)

then what happens? The coin follows the path that is the reflection of the path which it would have taken if there was no wall.

So instead of a single boring carrom board, we can imagine an infinite sequence of pairs of Holes as shown in the figure by me (to be uploaded)

So either it will fall on the above holes or the lower ones, Now this is easy

Suppose it strikes a upper hole, that would mean, that for some integers m and n we have

$mD\quad =\quad n(r)\quad -\quad \frac { 1 }{ 2 }$

where D is the width of board (1) and r is the distance covered by the coin horizontally in striking the upper wall and then cominb back down,

The 1/2 exists due to the fact that it didnt initially start from a hole

From initial conditions we easily have

$\\ D=1\\ \\ r=\frac { 11 }{ 15 }$

so we have on manipulating the expression we get

$\\ 15(2m+1)\quad =\quad 22n$

which is not possible because right side is odd whereas left side is even for all m and n

so neglect this possibilty,

Now think that it strikes an lower hole, so now i shift my start point to the first collision point for convenience and using similar logic i right

$mD\quad +\quad \frac { 2 }{ 15 } \quad =\quad n(r)$

(please understand why yourself, it is simple)

now manipulating it we get

$11n-2=\quad 15m$ which holds at m=5 and n=7

wonderful, this is what we seek!!

Now to count number of collisions we observe that it collides with vertical walls each time it crosses the boundary of holes (in our infinite sequence of carroms) and when it reflects of from the horizontal walls,

so answer is simply m +2n = 19

@Ronak Agarwal Am i correct ?

I built a simulation a while ago on Desmos Graphing Calculator. You can verify with this.

Julian Poon - 6 years, 3 months ago

I did too here

Dan Ley - 4 years, 4 months ago

For me I used the fact That : $\frac{y_{n+1}-y_{n}}{x_{n+1}-x_{n}} = (-m)^{n+1}$
Where $m= \frac{1-0}{2/15-1/2}$ Using This we calculate either $x_{n}$ or $y_{n}$ because either $0<x_{n}<1$ and $y_{n}=0$ or $y_{n}=1$ or the inverse using This I stopped when I got $x_{20}=1$ and $y_{20}=1$ which is one of the holes.

Oussama Boussif - 6 years, 3 months ago

ah, wonderful, the simple fact that the slope can only change its sign but never change in magnitude has been exploited, awesome that was, thanks for sharing !

Though i suppose you had to go all the way right? to 20

Mvs Saketh - 6 years, 3 months ago

Indeed, because You see it's hard to come up with a closed form formula since it's not predictable because for example y may either be 0 or 1 so that's fine, but the only problem is That y Will also have a value varying from 0 to 1 at some point which makes it harder to predict. My method was Just very long and bashy but yours is pretty good though I didn't know I had the right to break down the board into infinite ones.

Oussama Boussif - 6 years, 3 months ago

i already knew that but how can you go upto 19 terms , i went upto 17 terms and then gave up simply, bro our method has a great limitation. you had great stamina and did till 20 what if it went till 100 or 200 collisions ?

A Former Brilliant Member - 4 years, 9 months ago

That was beautiful! Took me a long time to convince myself that i can extend the board. Parallel mirrors! Even tried using constant slope logic, but that was a bit too tedious.

Raghav Vaidyanathan - 6 years, 3 months ago

Yes @Mvs Saketh that was my intended way. You posted the exact solution I had in my mind. Is this problem too easy. Mvs Saketh

Ronak Agarwal - 6 years, 3 months ago

Well i wouldnt say too easy, it takes some time to think

Mvs Saketh - 6 years, 3 months ago

But you can further simplify the problem by assuming a coordinate plane(for visualisation) use a graph paper write the equation of line from the initial values and find the lattice point in it. Infact there is no need to classify it into upper holes and lower holes. But +1 for solution

Ronak Agarwal - 6 years, 3 months ago

yes, the same logic of reflection could be used for upper holes.

Mvs Saketh - 6 years, 3 months ago

I'm not sure if this is what you're talking about, but I extended the line and then found the first lattice point at (-5, 15). Then, add a bounce for every line it intersects in the form y=n or x=n. Notice that the line intersects at n=0, -1..., -4 for the x=n's and n=1, 2, 3..., 14 for the y=n's. 14+5=19.

Is that what you had in mind?

Dylan Pentland - 6 years, 3 months ago

Exactly you are right

Ronak Agarwal - 6 years, 3 months ago

Beautiful question indeed !

@Ronak Agarwal you sure make some really good application based questions !

A Former Brilliant Member - 6 years, 3 months ago

Thanks for appriciating, by the way how you solved this problem.

Ronak Agarwal - 6 years, 3 months ago

I had taken help from a friend of mine to solve this question . Frankly even I don't know how he solved it !

A Former Brilliant Member - 6 years, 3 months ago

Hey i want to know one thing is there any way of finding derivative of sinx other than using limits.

Gautam Sharma - 6 years, 3 months ago

Yes, there is. You can write it as a polynomial approximation using taylor series. Differentiate it and you get $cosx$ .

Raghav Vaidyanathan - 6 years, 3 months ago

Nice solution! It took me some time to solve it as I messed around the same board instead of doing it that way.

Ayush Garg - 6 years, 3 months ago

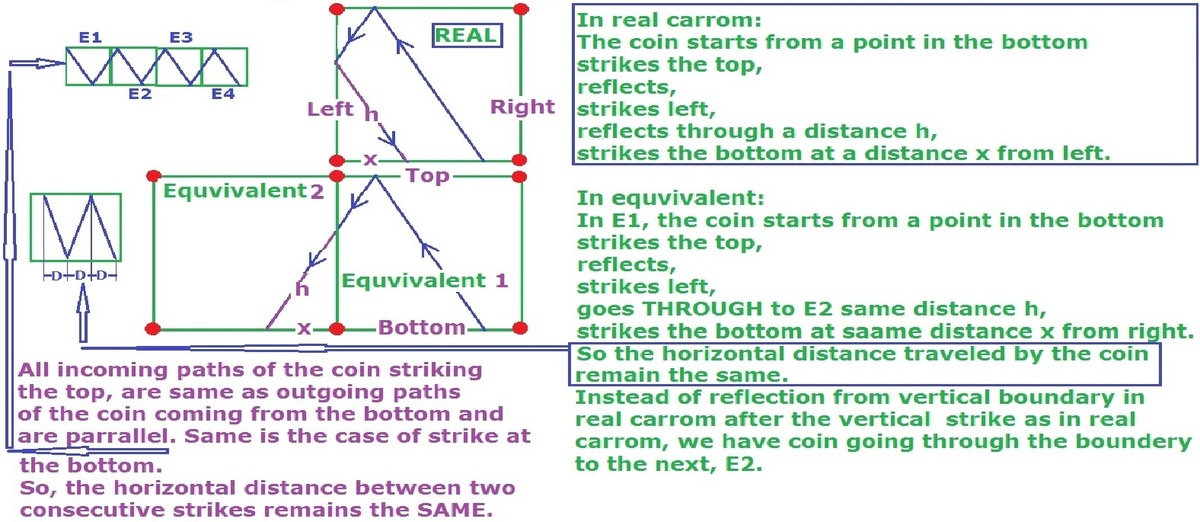
As mentioned by you, (Mvs Saketh ), the situation is equivalent to infinite boards to the left of first board. ( And their corners containing point holes. ) This means now in place of reflected paths from vertical sides, we have straight path to the next left board. And this simplifies our calculation.

I have shown above how a coin from bottom moves to the left after one strike at the top and second strike at the left. This is what is happening in problem on hand.
In general it can be easily seen how the coin would move if there are more top and bottom strikes and/or coin moving to the right, and/or starting from bottom and/or top, from the above explanation.

Let m be the number of horizontal strikes, n the number of equivalent boards, d the horizontal distance between horizontal strikes, v the number of common boundaries which is also the number of vertical strikes, and D the distance from start to the next boundary. H is the horizontal distance covered by the coin before it falls in the hole. B is the length of playing sides of the board.

$H=m * d~~~ but ~ also~~~ H= n * B - D.\\ \color{#3D99F6}{So~m * d = n * B - D. ~~~ We~ also~ have~ v=n-2.}\\ ~~~~\\ We ~are~ given~ B=1, D=1/2, \\ d=distance~between~ start~ point~ and~ first~ horizontal~ strike~ point = 1/2 - 2/15=11/30 \\ \implies~m * 11/30 = n * 1 - 1/2.~~~~\therefore 1 + \dfrac{11m}{15}=2n. \\ Since ~m,~ and~n ~are~integers, ~m~must~be~odd~multiple ~of~15.\\ Let~m=1*15.=15~~~~~~~~\therefore~n=6. ~and ~v=n-2=4.\\ Total ~strikes = m + v =\Large~~\color{#D61F06}{19}.$ ~

Niranjan Khanderia - 4 years, 1 month ago

Let's play carrom

This is original.

Image credit: Wikipedia Bernard Gagnon

The answer is 19.

1 solution

0 pending reports