Let's Play Chess on Other Planet
Consider a chess board. Let the total number of possible rectangles and squares be and respectively.
If the limit above is in the form of for coprime positive integers , find .
Details and Assumptions
- All squares are rectangles, but not all rectangles are squares.
Original
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
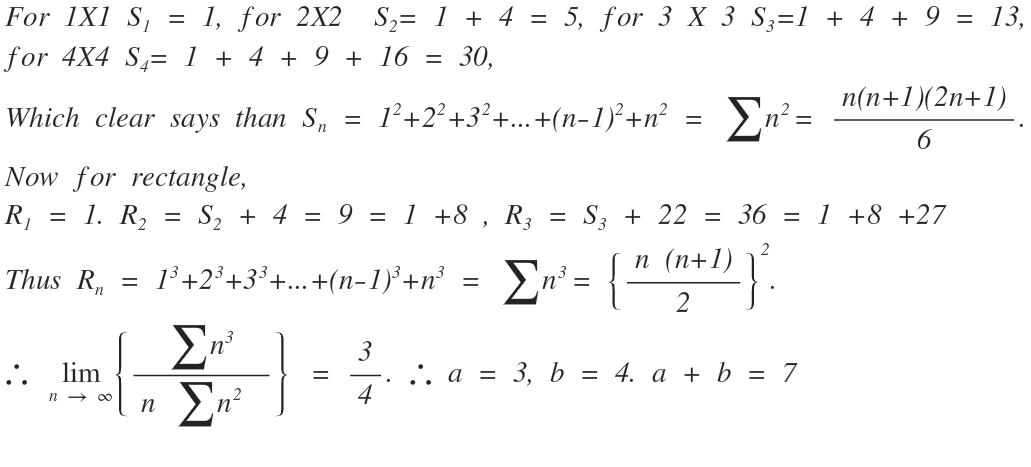
R n = ( n + 1 2 ) ( n + 1 2 ) = 4 n 2 ( n + 1 ) 2 S n = 1 ∑ n r 2 = 6 n ( n + 1 ) ( 2 n + 1 ) L = n → ∞ lim 2 ( 2 n + 1 ) 3 ( n + 1 ) = n → ∞ lim 2 ( 2 + n 1 ) 3 ( 1 + n 1 ) = 4 3
Here For calculating Rectangles There are n+1 Horizontal lines and n+1 vertical Lines so we select any two Vertical and any two horizontal Lines So that Rectangle is formed (and obviously squares are also rectangles)
You may Take Eg as Our Planet Chess Board ,(8*8) in This 9 are vertical and 9 horizontal lines are present.
Karan Keep it up bro ! Keep Posting such more :)