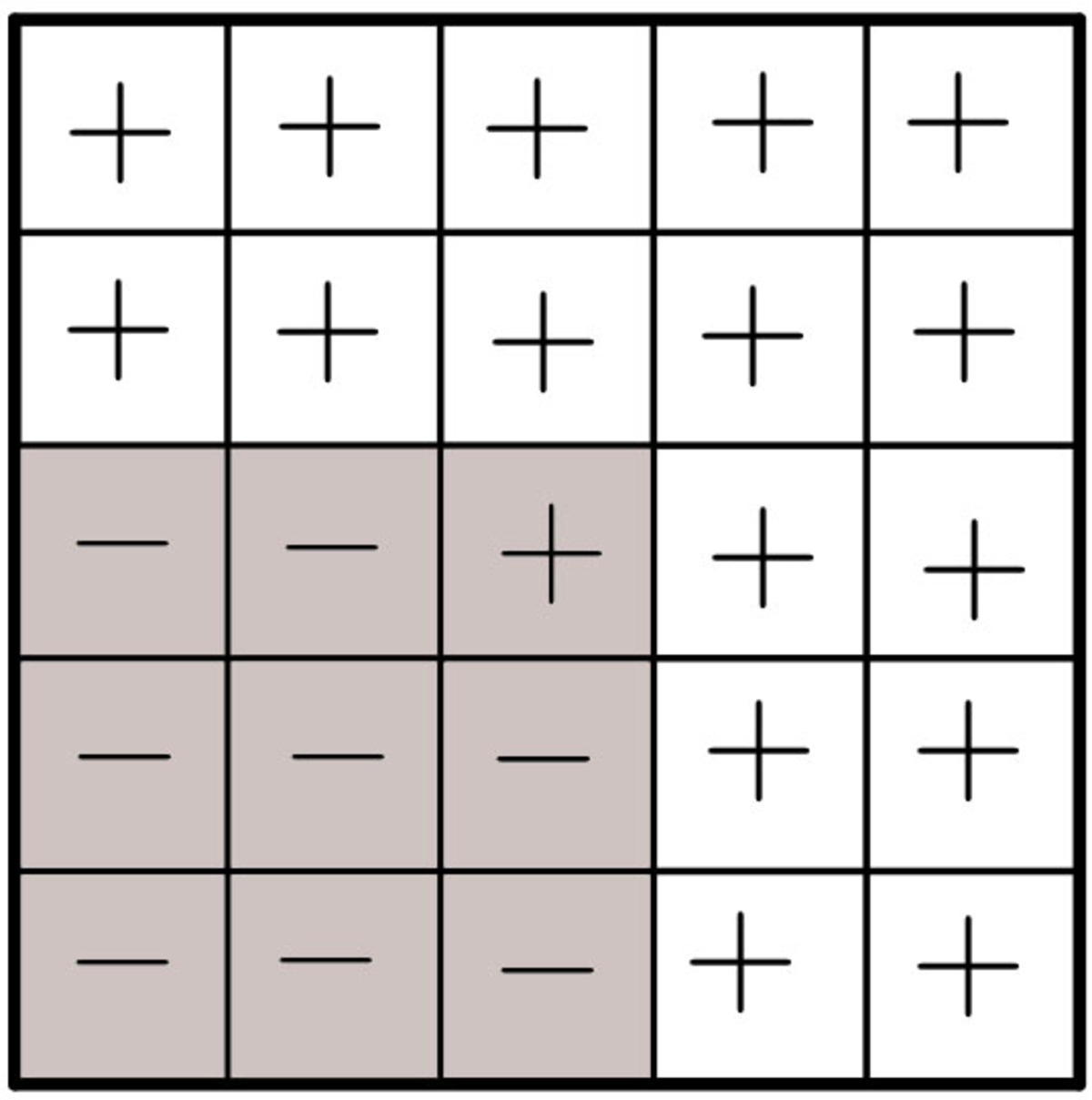
Let's play now
There is an square. Write a into 24 squares and one into 1 square, such that by using the step below as many times as you need, you can achieve that every square contains a .
Choose a or a square, and change each sign in the square (form to , and from to ).
How many places could be the in the beginning?
Note: Each square must contain exactly 1 sign.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Each square larger than a 1 × 1 square will contain an even number of blue squares. So if the - sign in the beginning is in a blue square, then after a step there will be an odd number of - signs in the blue area (it doesn't matter which type of square do we chose). Therefore the - sign will be on a yellow square.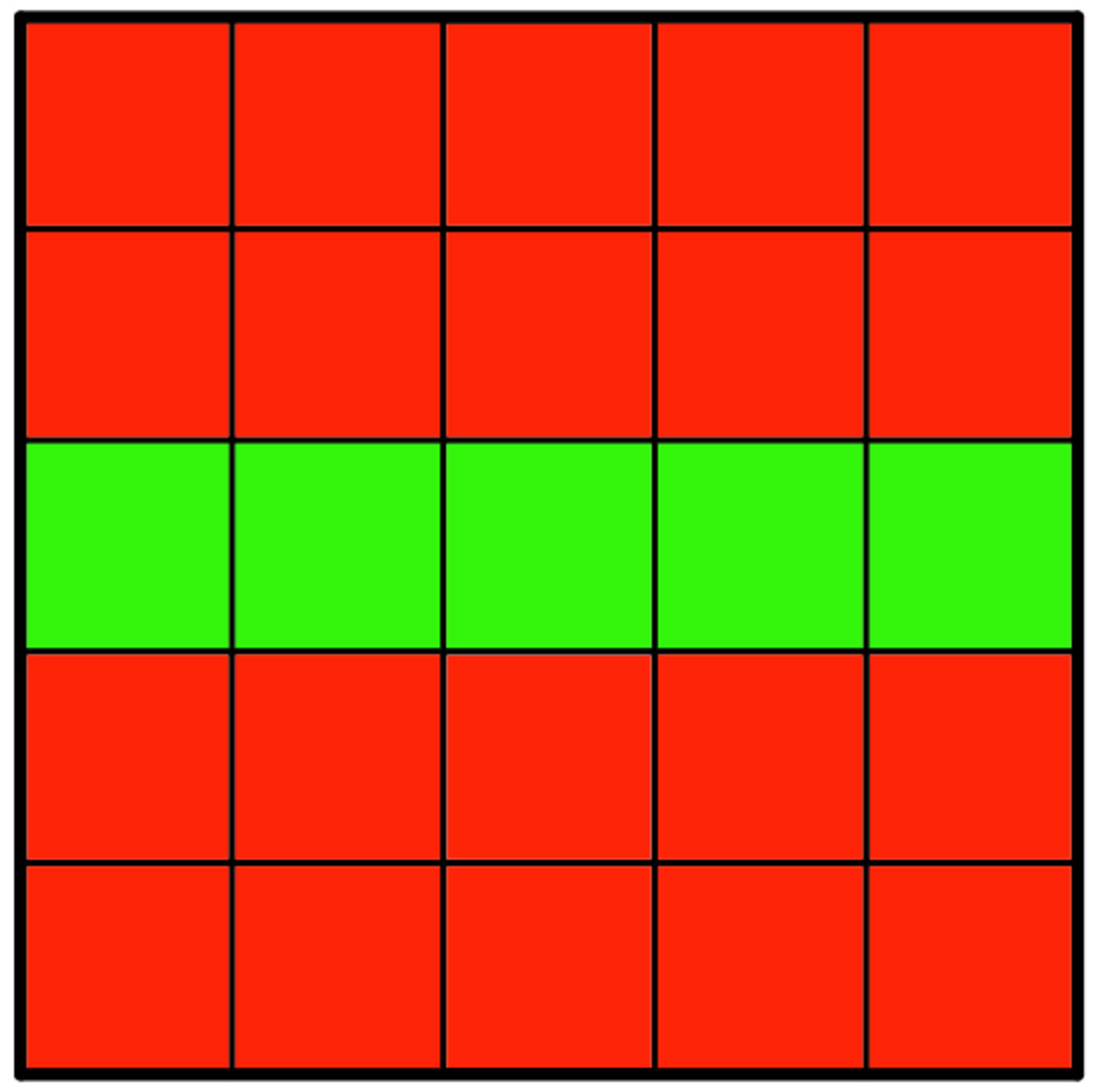
Each square larger than a 1 × 1 square will contain an even number of red squares. So if the - sign in the beginning is in a red square, then after a step there will be an odd number of - signs in the red area (it doesn't matter which type of square do we chose). Therefore the - sign will be on a green square.
There is only one square, which is in both of the yellow and the green areas: the middle 1 × 1 square. Here is an example: