Let's play pool
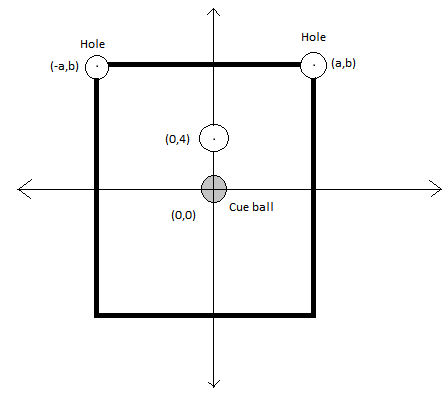 A pool table is set up on a co-ordinate plane as shown in the figure. A cue ball of radius
is placed with it's centre at the origin.Also the there are only two holes in the table each of radius
with their centres at
and
respectively.
A pool table is set up on a co-ordinate plane as shown in the figure. A cue ball of radius
is placed with it's centre at the origin.Also the there are only two holes in the table each of radius
with their centres at
and
respectively.
The ball which is to be shot into the hole is of radius and is placed with it's centre at .
If the possible values of for which it is possible to shoot the ball into the hole is that is . Then find .
Details and Assumptions
1) ,Mass of both the balls is same.There is no friction on the table
2)The collision of the cue ball with the given ball is elastic.
3)The ball has to be directly shot into the hole.No bouncing with the sides of the pool table is allowed.
4)c,d are denoting the end-points of the range y is belonging to.
Sorry by mistake in the figure the co-ordinates of the ball is shown to be (0,4). It is actually (0,y)
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First the centre of the ball is marked as point B, the origin as O, and the centre of the cue ball at the time when it hits the ball be A.
Now if the cue ball is able to hit the ball into the hole then the neccasary and sufficient condition is ∠ A B O > 9 0 0
First in the triangle A B O , A B = 2 r , O B = y and we assume A O = x
Applying cosine rule we have :
c o s ( ∠ B A O ) = 4 r x 4 r 2 + x 2 − y 2 < 0
⇒ 4 r 2 + x 2 < y 2 ( i )
Again applying cosine rule we have :
c o s ( ∠ O B A ) = 4 r y 4 r 2 + y 2 − x 2
⇒ x 2 = 4 r 2 + y 2 − 4 r y c o s θ ( θ = ∠ O B A ) ( i i )
Using (ii) in (i) we have :
4 r 2 + 4 r 2 + y 2 − 4 r y c o s θ < y 2
⇒ 2 r < y c o s θ ( i i i )
(Refer to the diagram) In the right triangle BDE we have :
c o s ( ∠ D B E ) = c o s θ = B E B D
Put the values of BD and BE we get
c o s θ = a 2 + ( b − y ) 2 b − y ( i v )
Using (iv) in (iii) we get :
2 r a 2 + ( b − y ) 2 < y ( b − y ) (v)
⇒ ( y 2 − 4 r 2 ) ( y − b ) 2 > 4 r 2 a 2
Put the values to get :
( y 2 − 1 ) ( y − ( 2 9 + 5 ) ) 2 > 2 1 5 ( 3 + 5 )
Solving for the inequality we have y ϵ ( 2 , 4 ) .
Hence c = 2 , d = 4 hence c 2 + d 2 = 2 0