Let's See if You Have Geometry Reasoning
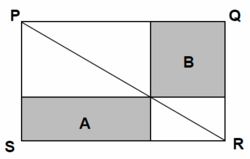 If PQRS is a rectangle and if 'A' and' B' represent the shaded areas (in the diagram above), which of the following statements is true?
If PQRS is a rectangle and if 'A' and' B' represent the shaded areas (in the diagram above), which of the following statements is true?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Great problem. Loved it :)
Log in to reply
Hey Calvin ! how are you ? I see you're master in Mathematics how you became good in Maths . give me some tips , I follow your answer always
Log in to reply
Keep on practicing and improving regularly. Work on the "Problems of the day", which will help you get better over time. Read up on the wikis to learn about these techniques that interest you.
Your method is much better than mine! :D
great solution
but if PS=5 ,SR=10,SH=7 then IG becomes 3 if IH=2,then IF =3 which is not satisfying the condition
See Mark's image for the notation to use.
- Note that PE = IF and GI = HR .
- Note that the triangles PEI and IHR are similar.
- Therefore, EI PE = HR IH
- By above, EI IF = GI IH
- By cross multiplication , IF × GI = IH × EI , which is the result wanted,
- since the area of A is IH × EI ,
- and the area of B is IF × GI .
Any diagonal of a rectangle divides it in half. Therefore, the area of PRS equals the area of PRQ; and the area of PIE equals the area of PIF and the area of IGR equals the area of IHR. Since PQR is equal to PRS and if you remove the above noted equal areas from each, then the two areas left, A and B, must be equal.
Please refer to the figure shown by Mark Mottian: PEI+A+RHI = PFI+B+RGI Equation (1) Since: PEI = PFI Equation (2) RHI = RGI Equation (3) Substitute Equation (2) & (3) in Equation (1`) PEI + A + RHI = PEI + B + RHI Cancel: PEI, RHI Therefore: A = B
If we try to visualise triangle psr and pqr can be proved congurent by SAS and the triangles forming within these triangle (unshaded area )Are congurent now if equal are if taken off from congurent triangle the left area if also equal . We can prove the congruence easily and it is visible very much i hope i dont need to explain that
In a short, rough, unofficial, initial analysis, I have concluded that: EI > FI > IG > IH (use sir Mark Mottian's image of solution as reference since I have only judged it mentally, so, there is no drawing / image to upload.) Then, the two rectangles are being separated by a diagonal inside a rectangle. Area of Rectangle EISH = (EI)(IH) and Area of Rectangle FQIG = (FI)(IG). Rectangle EISH uses the longest and the shortest division of the proportion (Extremes), and Rectangle FQIG uses the 2nd and 3rd longest division (Means), so I have concluded that they must be equal. (Though I still tried to properly solve it using ratio and proportion like what sir Mark did to confirm if I am indeed correct, and, I am.) This is only possible because the two rectangles were separated by the diagonal inside of the biggest rectangle. I apologize for my bad and confusing grammar, though.
No trig PSR and trig POR will be equal. the left over traingles wil be same area , hence A =B
See Mark's image for the notation to use. Consider rectangle IGRH, and let that have area C.
By similar triangles, P S I H = S R H R .
Hence, A C = S R H R = F H I H = B C .
Thus, A = B .
Let [ABC] denote the area of ABC
The diagonal PR divides the entire rectangle in half: [PSR] = [PQR]
So, [PEI] + [ESHI] + [IHR] = [PFI] + [FQGI] + [GIR]
The diagonal also divides two smaller shaded regions in half: [PEI] = [PFI] And [GIR] = [IHR]
It follows that [ESHI] = [FQGI] Or [A] = [B]
PLEASE LIKE AND RESHARE