Let's think out of the box
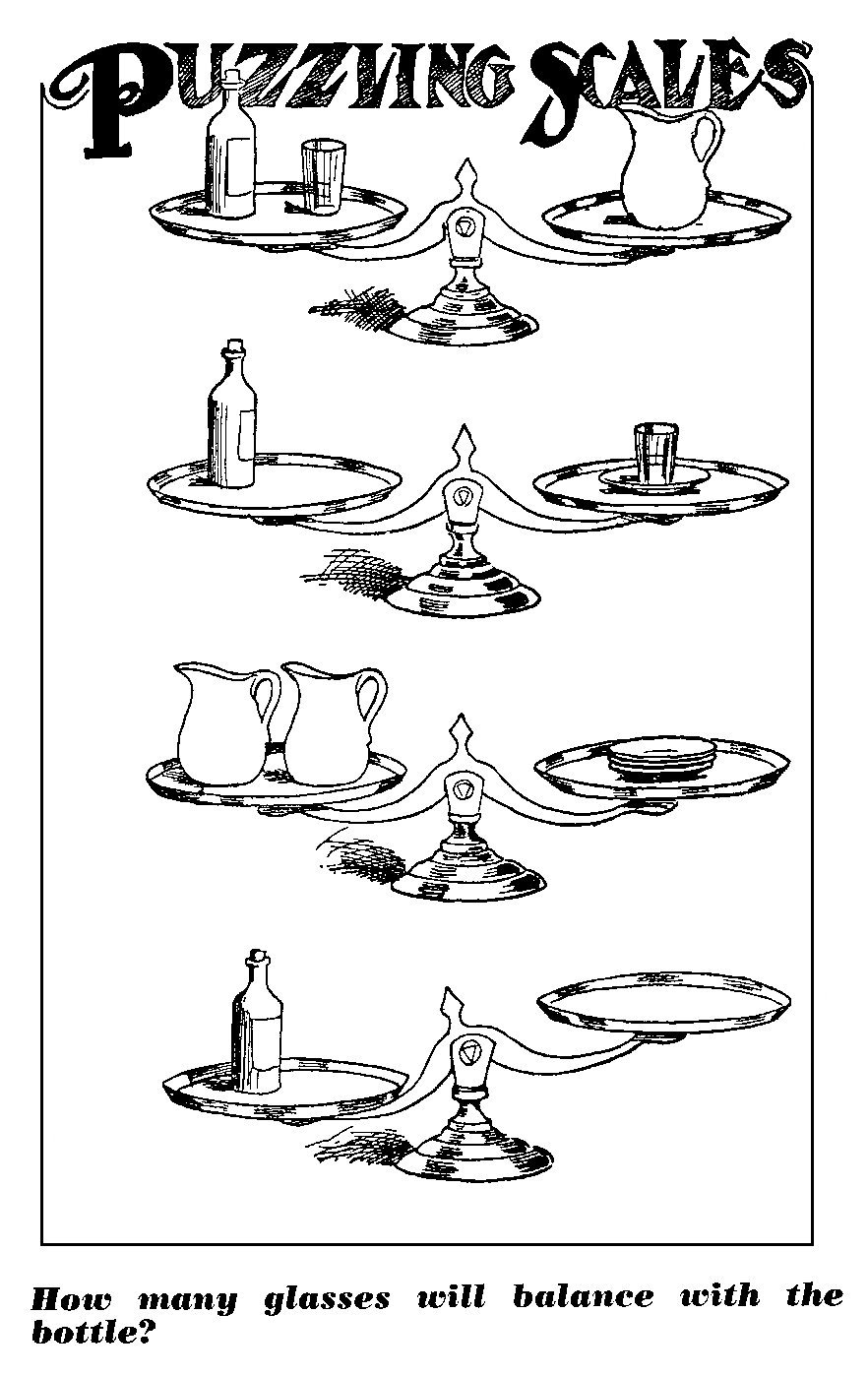
A bottle and a glass balances the jug. A bottle balances a plate and a glass. Two jugs balances 3 plates. From the given conditions, find out how many glasses will balance the bottle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let us denote the bottle by B , jug by J , plate by P and glass by G .
So from the first statement,
B + G = J . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
From the second statement,
P + G = B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
From the third statement,
3 P = 2 J
or, P = 3 2 J . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
Putting value of \boxed{3}) in \boxed{2})
B = 3 2 J + G
or, 3 B = 2 J + 3 G
or, 3 B = 2 B + 2 G + 3 G ....(putting value from 1
or, B = 5 G