Letters are to arranged in box ..............

Probability Level 4

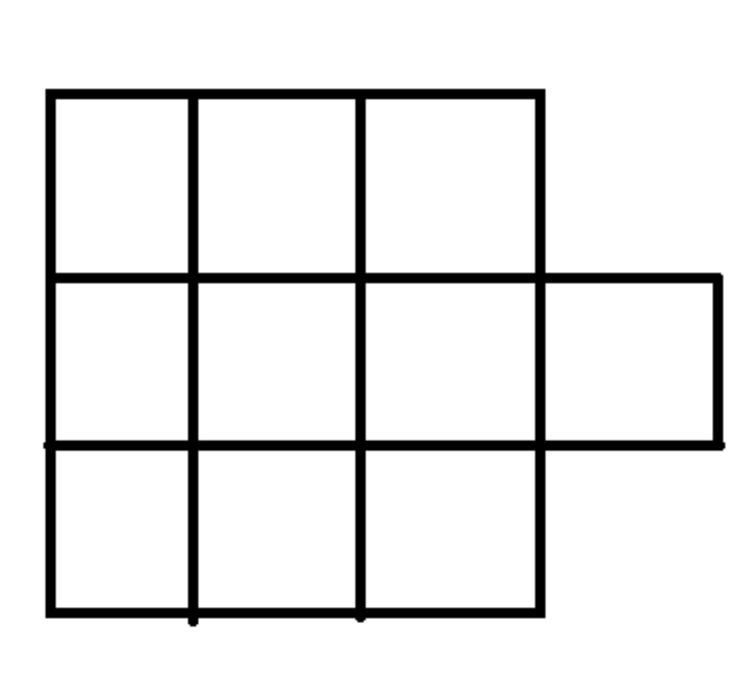The number of ways in which 7 different letters can be arranged in the figure such that no row is empty is

59*k * 7!

Then value of k is _ __


The answer is 2.

Arpit Dhimanj by Arpit Dhimanj , 23, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Arpit Dhimanj
Jul 3, 2014

Answer 2

Required number of ways = Total - when one row is empty ( either 1st or 3rd ) = C(10,7) . 7! - C(2,1) . 7! = 58 . 2 . 7!

2 Helpful 0 Interesting 0 Brilliant 0 Confused

How is it C(2,1) In second case?

Jayakumar Krishnan - 6 years, 11 months ago

First, i thought the '7' is not factorials so my anwer was 1440 than 720 but in my last chances i see it. Just want to make everybody more careful to take steps...

Hafizh Ahsan Permana - 6 years, 11 months ago

I chose 3 out of the 7 distinct letters in 7C3 ways then sent one of them to 1st row, one to 2nd row, one to the 3rd row, they can arrange among themselves in 6 ways, so (7.6.5) ways till now.., now we have 7 spaces left, and 4 letters left, so choose any 4 of the 7 places 7C4 and then fill them in 4! ways, so (7.6.5.4) ways of this.., total ways = (7.6.5)(7.6.5.4) = (7.6.5.4.3.2.1)(7.5.4) = (140)7! ... but where is the mistake?

Jayant Kumar - 6 years, 11 months ago

By putting 7 letters into this figures, from pigeonhole principle, there must exist at least 1 letter on the 2nd row (horizontal). So you don't have to consider the 2nd one.

And we can also see that the 1st row and 3rd row can't be empty at the same time, so those 2 events are mutually exclusive. (no need to consider both of them happening at the same time.)

Here's what we're going to do...

Number of ways = Total ways - 1st row empty - 3rd row empty

Total ways:

  • Choosing 7 spots from 10 spots, ( 10 7 ) \dbinom{10}{7} .
  • 7 letters are different, 7 ! 7! .

Total ways = ( 10 7 ) 7 ! \dbinom{10}{7}7!

1st row empty, 3rd row empty (same number of ways)

  • 7 letters are different, 7 ! 7! .

Therefore, the number of ways

= ( 120 − 2 ) × 7 ! = 59 × 2 × 7 ! = (120 - 2)\times 7! = 59\times 2 \times 7!

k = 2 k = \boxed{2} . ~~~

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...