Lexical Number Theory
Assume that the strings accepted by the automata below are interpreted as binary numbers .
What is the largest integer such that the set of integers accepted by the automata are always divisible by ?
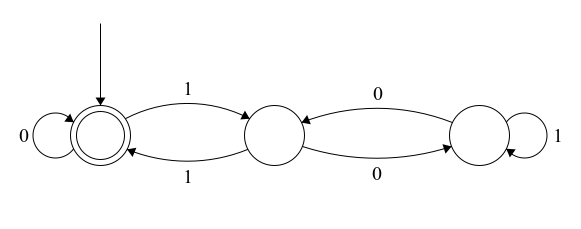
Extra Credit: Prove your answer.
Extra Extra Credit: Is it always possible to form such an automata, for any ? If not, why not? If yes, how?
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let's name the states as follows: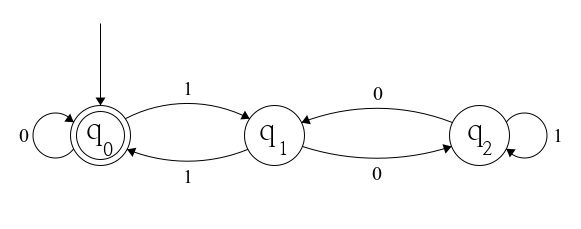
Now, we claim that after scanning a binary string x , the auomaton is in the state q ( x m o d 3 ) . That'd entail that the accepted strings are ≡ 0 ( m o d 3 )
We start with two observations:
The last piece of observation can be proven only through manual verification and is the key to the solution. In fact, the diagram is just a more complex way to represent the above transition function.
The rest of the proof follows from induction
Thus, for any string x , the auomaton is in the state q ( x m o d 3 ) . QED
The major trick in the design of the automaton is that the transition function can be defined as δ ( q n , c ) = 2 n + c m o d 3 .
So yes, we could design automatons to test the divisibility by any natural number d and in any base b with a d state automata with the transition function defined as δ ( q n , c ) = b n + c m o d d .
Here is an automata that checks divisiblity by 5
This StackOverflow thread explains the principle in more detail.
[1] For simplicity, we choose that the empty string ϵ is interpreted as 0