Light Beam - Minimum Travel Time
A beam of light travels through a compound dielectric slab along two straight line segments from the start point to the end point, as shown. The " " quantities are the speeds of the light beam in the two regions.
Suppose that the light travels along a path which minimizes the total travel time. When the light gets to the boundary between the two dielectric regions, what is its coordinate?
Inspired by a comment from Karan Chatrath
Note: As it turns out, this is actually how light behaves within a compound dielectric slab. From this "least time" principle, we can derive various well-known optical properties.
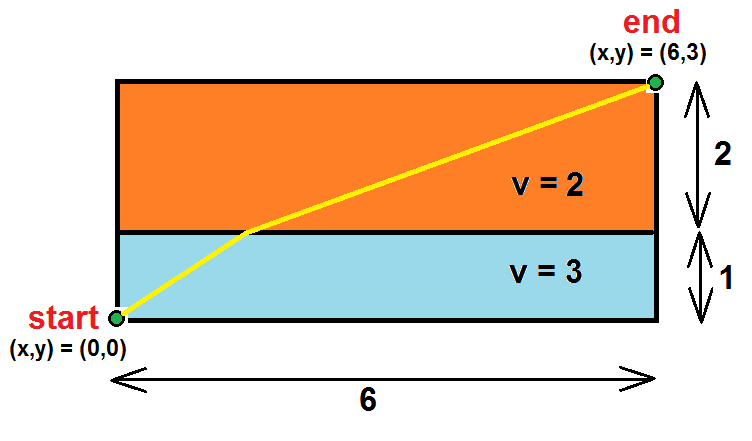
The answer is 4.2926.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 1 √( x 2 +1)+ 2 1 √(( 6 − x ) 2 +4)=minimum. Therefore 5 x 4 -60 x 3 +173 x 2 -108x+324=0. The real solution to this equation less than 6 is x=4.29259