Like a pyramid but not quite
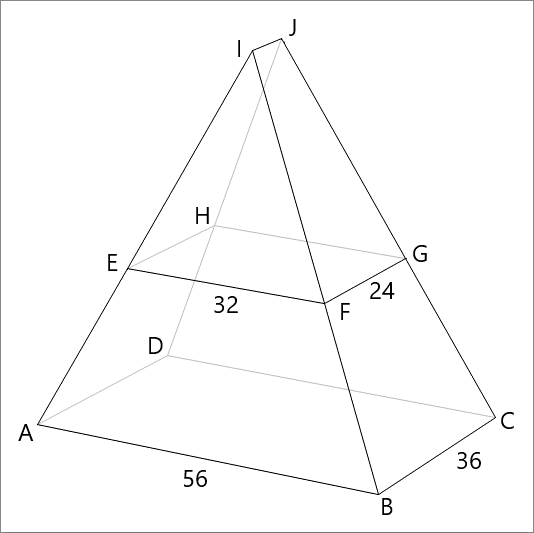
Polyhedron A B C D - E F G H has the bottom rectangle A B C D measuring 5 6 × 3 6 and top rectangle E F G H measuring 3 2 × 2 4 . The two rectangles are aligned, with the longer edges parallel to the x -axis, and the shorter edges parallel to y -axis, and their centers lying on the vertical z -axis with a vertical separation of h = 2 4 .
Now the planes connecting the two rectangles are extended, so that they form the polyhedron E F G H - I J on top of rectangle E F G H . Find the volume of polyhedron E F G H - I J . The volume can be written as V = N + 3 1 , where N is a positive integer. Enter N as your answer.
The answer is 9557.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Excellent geometric solution, one that does not use calculus. Thanks for taking the time to share it.
Taking a horizontal cross section of polyhedron E F G H − I J at elevation z , it will be a rectangle having dimensions L ( z ) × W ( z )
The length L ( z ) = 5 6 + h ( 3 2 − 5 6 ) z = 5 6 − z , and the width W ( z ) = 3 6 + h 2 4 − 3 6 z = 3 6 − 2 1 z
Hence, the volume is given by V = ∫ h 5 6 A ( z ) d z = ∫ 2 4 5 6 ( 5 6 − z ) ( 3 6 − 2 1 z ) d z
The integral is straightforward to perform and yields, V = 9 5 5 7 3 1 . Thus, N = 9 5 5 7
Since 5 6 3 2 = 3 6 − x 2 4 − x solves to x = 8 , that means I J = 8 , and we can take out a triangular prism cross-section with a lateral height of 8 from E F G H − I J and combine the remaining sections to create a pyramid with a 3 2 × 1 6 rectangular base:
By proportions, the height h of the pyramid fulfills 5 6 3 2 = h + 2 4 h , which solves to h = 3 2 .
Therefore, the volume of E F G H − I J is V = V pyr + V prism = 3 1 ⋅ 3 2 ⋅ 1 6 ⋅ 3 2 + 2 1 ⋅ 3 2 ⋅ 3 2 ⋅ 8 = 9 5 5 7 + 3 1 .