Like a Rolling Stone!
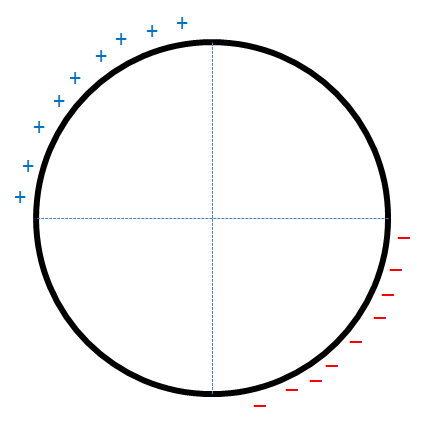 The figure shows a non-conducting, non-uniformly charged ring with linear charge densities
and
, mass
and radius
. This ring is placed on a rough horizontal surface and a horizontal electric field
is switched on.
The figure shows a non-conducting, non-uniformly charged ring with linear charge densities
and
, mass
and radius
. This ring is placed on a rough horizontal surface and a horizontal electric field
is switched on.
If at some instant, the ring is in the position shown above and is rolling without slipping, find the minimum coefficient of friction required.
Details & Assumptions
- A uniform gravitational field acts downward.
The answer is 0.314.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
+ d q = λ R d θ ; d ⊥ = R ( 1 + cos θ ) ; d F + = + d q ⋅ E ⟹ d τ = d F + ⋅ d ⊥ = λ R 2 E ( 1 + cos θ ) d θ
τ + = ∫ 0 2 π λ R 2 E ( 1 + cos θ ) d θ = λ R 2 E ( 2 π + 1 )
− d q = − λ R d θ ; d ⊥ = R ( 1 − cos θ ) ; d F − = − d q ⋅ E ⟹ d τ = d F − ⋅ d ⊥ = − λ R 2 E ( 1 − cos θ ) d θ
τ − = − ∫ 0 2 π λ R 2 E ( 1 − cos θ ) d θ = − λ R 2 E ( 2 π − 1 )
Apply Newton's Second Law to the rotation:
τ + + τ − = I O ⋅ α , where I O is the ring's moment of inertia with respect to O : I O = m R 2 + m R 2 .
2 λ R 2 E = 2 m R 2 ⋅ α ⟹ α = m λ E ⟹ a = α R = π s 2 m
Apply Newton's Second Law to the translation (notice that the electric forces cancel out in this case):
μ m i n m g = m a ⟹ μ m i n = g π ≈ 0 . 3 1 4