Like Triangles, Then take this!!
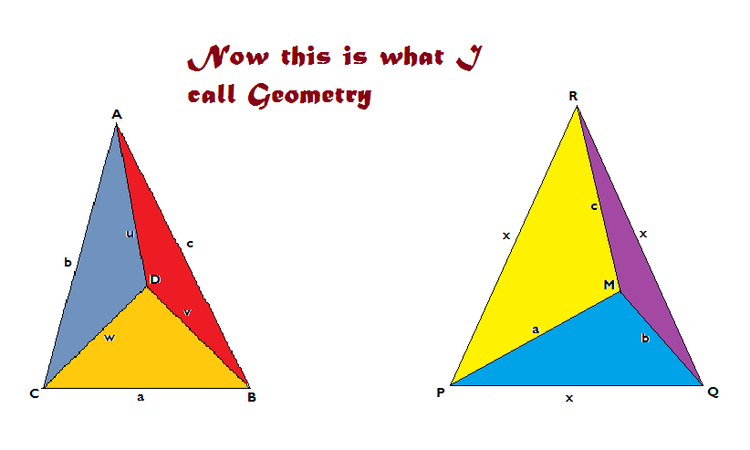 Consider two triangles ABC and PQR such that
In order to rotate the two figures we rotate PRQM by an angle
clockwise about Q to obtain RR'QM' .
Again let X and Y be points on RQ and PQ such that M lies on XY parallel to PR;
Consider two triangles ABC and PQR such that
In order to rotate the two figures we rotate PRQM by an angle
clockwise about Q to obtain RR'QM' .
Again let X and Y be points on RQ and PQ such that M lies on XY parallel to PR;
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
0 solutions
No explanations have been posted yet. Check back later!