Aly's Limit Problem

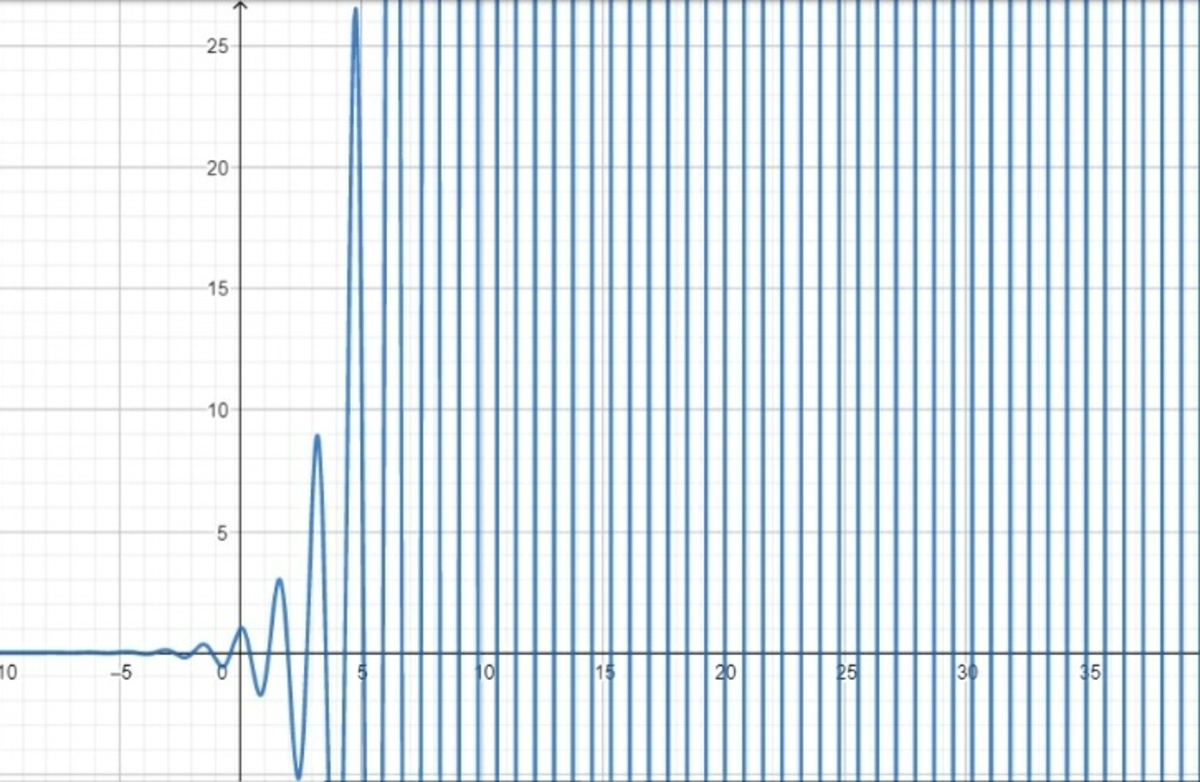
Assume that the function has a limit $c$ when $x$ approaches infinity. Then, $\lim_{x\to \infty} 2^x \cos (4x)=c$ By the definition of limit, there exists an interval $(\epsilon, \infty)$ such that, for all values of $x \in (\epsilon, \infty)$ , the function $2^x \cos (4x)$ approaches (is close to) $c$ . But no matter how large $\epsilon$ might be, for some sufficiently large $n$ , the interval contains $a=\frac{(2n+\frac{1}{2})\pi}{4}$ $b=\frac{2n\pi}{4}$ Since $2^a\cos (4a)=0$ and $2^b\cos (4b)=2^b$ , this is a contradiction. Therefore, the limit does not exist.

Note: The function shows oscillatory behavior and does not approach a fixed value. The graph below is a clear illustration of this claim.

Claim : The limit does not exist.

Proof: Suppose not. That is, suppose it exists. Then the limit of all its subsequences also exists.

If we take $x$ as any multiple of $\pi$ , then the subsequence is always a positive number.

If we take $x$ as $\pi \cdot k + \frac\pi 4$ , where $k$ is any integer, then the subsequence is always a negative number.

This means that as $x$ becomes unboundedly large, the expression always fluctuates violently between positive numbers and negative numbers. A contradiction!