Limit

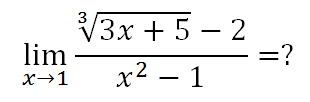
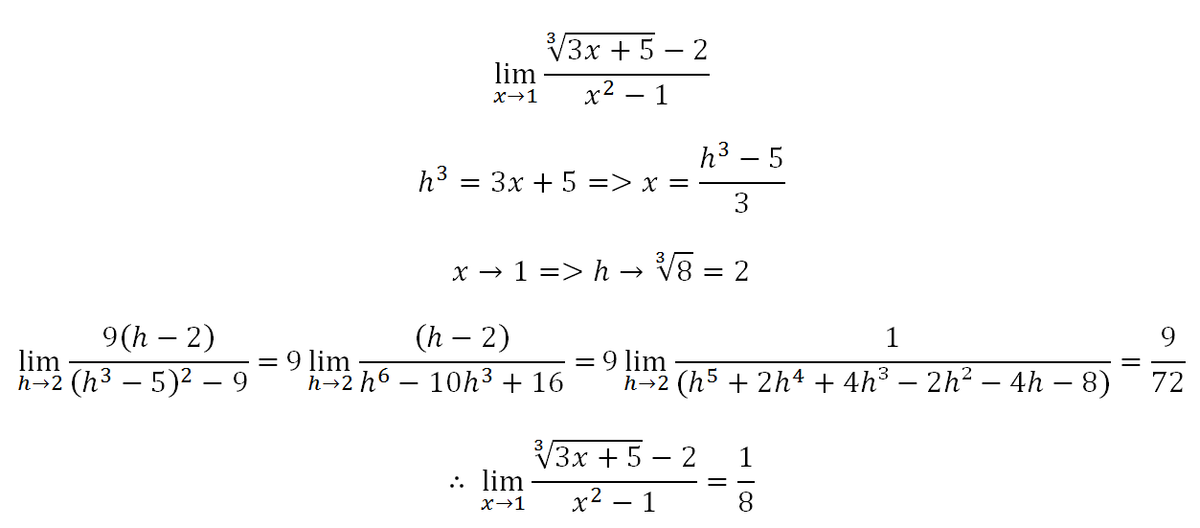
When we try to plug in 1, we end up with the indeterminate form $\frac{0}{0}$ :

$\frac{\sqrt[3]{3+5} - 2}{1^2-1} = \frac{0}{0}$

This means we can try to evaluate the limit using L'Hopital's rule by replacing the numerator and the denominator with their derivatives. The derivative of $\sqrt[3]{3x+5} - 2$ can be calculated more easily if we translate it to its power form $(3x+5)^{\frac{1}{3}} - 2$ . We can apply the chain and power rules here and say that the derivative of the numerator is $\frac{1}{3}(3x+5)^{-\frac{2}{3}} \times 3 = (3x+5)^{-\frac{2}{3}}$ . Power rule says that the derivative of the denominator is $2x$ .

So we're left with:

$\lim_{x \to 1} \frac{(3x+5)^{-\frac{2}{3}}}{2x} = \frac{\frac{1}{4}}{2} = \boxed{\frac{1}{8}}$

Algebric solution: