Limit and Geometry 001
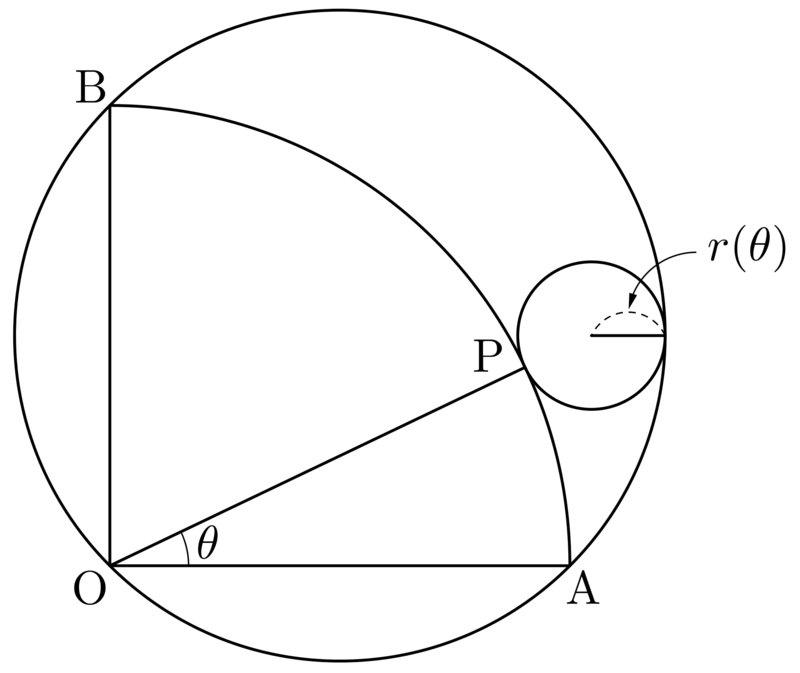
There is a quarter circle O A B inscribed in a unit circle as shown in the diagram. Let P be a point on arc A B that satisfies ∠ P O A = θ , and r ( θ ) be the radius of the circle that is tangent to arc A B at point P and also internally tangent to the unit circle.
What is the value of the limit θ → 0 + lim θ r ( θ ) ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
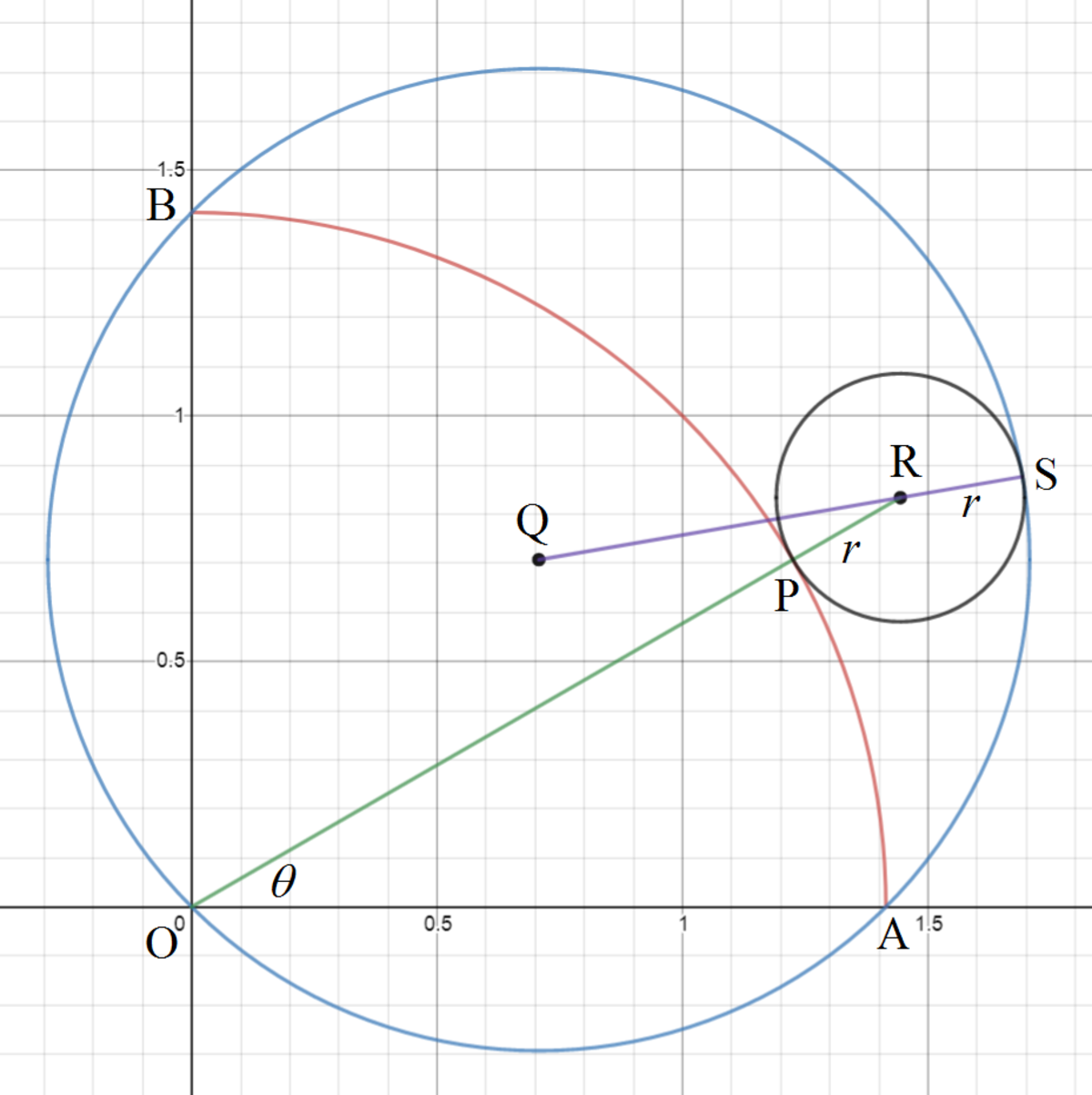
Let O be the origin ( 0 , 0 ) of the x y -plane. Then O A and O B are two sides of the square inscribed in the unit circle. Since A B = 2 , O A = O B = 2 = O P . The center of the unit circle is Q ( 2 1 , 2 1 ) . Let the center of the circle tangent to the arc A B and unit circle be R . Then O R = O P + P R = 2 + r ( θ ) and R ( ( 2 + r ) cos θ , ( 2 + r ) sin θ ) . We note that Q S = 1 since it is a radius of the unit circle. Then Q R = Q S − R S = 1 − r ( θ ) . By Pythagorean theorem :
( ( 2 + r ) cos θ − 2 1 ) 2 + ( ( 2 + r ) cos θ − 2 1 ) 2 ( 2 + r ) 2 − 2 ( 2 + r ) ( sin θ + cos θ ) + 1 r 2 + 2 2 r + 2 − 2 ( 2 + r ) sin ( θ + 4 π ) ( 2 + 1 − sin ( θ + 4 π ) ) r ⟹ r ( θ ) = ( 1 − r ) 2 = r 2 − 2 r + 1 = r 2 − 2 r = 2 sin ( θ + 4 π ) − 1 = 2 + 1 − sin ( θ + 4 π ) 2 sin ( θ + 4 π ) − 1
Therefore
θ → 0 + lim θ r ( θ ) = θ → 0 + lim θ ( 2 + 1 − sin ( θ + 4 π ) ) 2 sin ( θ + 4 π ) − 1 = θ → 0 + lim 2 + 1 − sin ( θ + 4 π ) − θ cos ( θ + 4 π ) 2 cos ( θ + 4 π ) = 2 + 1 − 2 1 1 = 2 + 2 − 1 2 = 2 + 1 2 = ( 2 + 1 ) ( 2 − 1 ) 2 ( 2 − 1 ) = 2 − 2 A 0/0 case, L’H o ˆ pital’s rule applies. Differentiate up and down w.r.t. θ .
Reference: L'Hôpital's rule
Let O 1 be the center of the unit circle and let O 2 be the center of the circle of radius r ( θ ) .
O O 1 = 1 , O O 2 = 2 + r , O 1 O 2 = 1 − r
∠ O 1 O O 2 = ∠ O 1 O A − ∠ P O A = 4 π − θ
Apply cosine rule to triangle O O 1 O 2 , and we get the following equation.
O 1 O 2 2 = O O 1 2 + O O 2 2 − 2 O O 1 × O O 2 cos ( ∠ O 1 O O 2 )
⇒ ( 1 − r ) 2 = 1 + ( 2 + r ) 2 − 2 ( 2 + r ) cos ( 4 π − θ )
⇒ r ( θ ) = 2 + 1 − cos ( 4 π − θ ) 2 cos ( 4 π − θ ) − 1 = 2 + 1 − cos ( 4 π − θ ) cos θ + sin θ − 1
(Angle sum identity was used in the last equality.)
Now we can evaluate the limit.
θ → 0 + lim θ r ( θ ) = θ → 0 + lim ( θ sin θ + θ cos θ − 1 ) × θ → 0 + lim 2 + 1 − cos ( 4 π − θ ) 1
= ( 1 + 0 ) × 2 2 + 1 1 = 2 − 2