Limit and Geometry 002
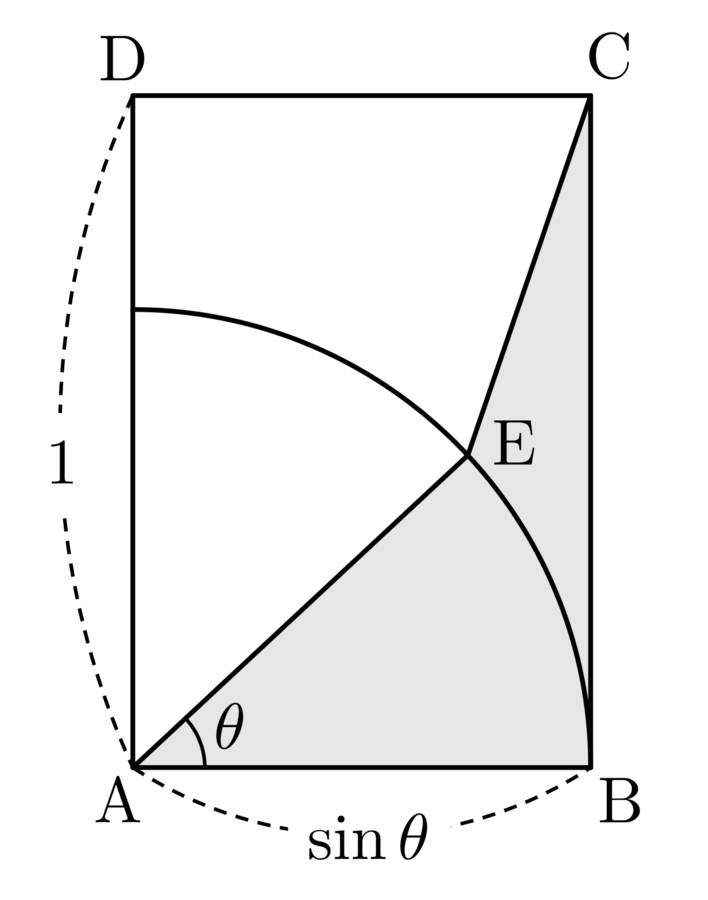
As shown in the diagram, rectangle A B C D has side lengths A B = sin θ and A D = 1 . Point E inside rectangle A B C D is such that A E = A B and ∠ E A B = θ .
If S ( θ ) is area of quadrilateral A B C E , find θ → 0 + lim θ 3 S ( θ ) .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
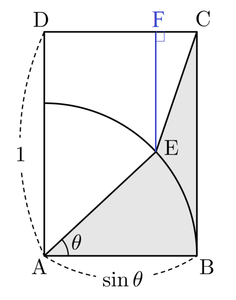
Note that S ( θ ) = [ A B C E ] = [ A B C D ] − [ A E C D ] . To find [ A E C D ] , draw E F ∣ ∣ A D . Then:
S ( θ ) = [ A B C D ] − [ A E C D ] = [ A B C D ] − [ A E F D ] − [ C E F ] = A D × A B − 2 ( A D + E F ) × D F − 2 C F × E F = A D × A B − 2 A D × D F − 2 C D × E F = sin θ − 2 sin θ cos θ − 2 sin θ ( 1 − sin 2 θ ) = 2 sin θ ( 1 − cos θ + sin 2 θ ) = 4 2 sin θ − sin 2 θ + 2 sin 3 θ
Therefore,
θ → 0 + lim θ 3 S ( θ ) = θ → 0 + lim 4 θ 3 2 sin θ − sin 2 θ + θ → 0 + lim 2 1 ( θ sin θ ) 3 = θ → 0 + lim 1 2 θ 2 2 cos θ − 2 cos 2 θ + 2 1 ⋅ 1 3 = θ → 0 + lim 2 4 θ − 2 sin θ + 4 sin 2 θ + 2 1 = θ → 0 + lim 2 4 − 2 cos θ + 8 cos 2 θ + 2 1 = 2 4 6 + 2 1 = 4 3 A 0/0 case, L’H o ˆ pital’s rule applies. After differentiation, again 0/0 Again a 0/0 case Differentiate up and down w.r.t. θ
I calculated the limit more or less the same way(I applied L'Hospital's thrice), but I found the area differently: I let F be the foot of the altitude from E and split it into the area of two triangles( △ A B E and △ B E C ), which can be computed using trigonometry on △ A E F and 2 1 ⋅ b ⋅ h .
Draw a line segment from E till it intersects AB at F, which is perpendicular to AB. Draw a line segment from E till it intersects BC at G, which is perpendicular to BC. Then, the shaded area is the following:
S = A r e a ( △ A E F ) + A r e a ( △ E G C ) + A r e a ( E F B G )
E F B G is a rectangle. Let sin θ = r . Then the expression comes out to be:
S = 2 r 2 sin θ cos θ + 2 1 ( r − r cos θ ) ( 1 − r sin θ ) + ( r sin θ ) ( ( r − r cos θ )
This expression can be simplified to obtain the following:
S = 2 sin 3 θ cos θ + sin θ ( 1 − cos θ ) ( 1 − sin 2 θ ) + 2 sin 2 θ ( 1 − cos θ )
S = 2 sin 3 θ cos θ + sin θ ( 1 − cos θ ) cos 2 θ + 2 sin 2 θ ( 1 − cos θ )
Therefore:
θ → 0 + lim θ 3 S = θ → 0 + lim 2 θ 3 sin 3 θ cos θ + sin θ ( 1 − cos θ ) cos 2 θ + 2 sin 2 θ ( 1 − cos θ )
θ → 0 + lim θ 3 S = ( θ → 0 + lim 2 θ 3 sin 3 θ cos θ ) + ( θ → 0 + lim 2 θ 3 sin θ ( 1 − cos θ ) cos 2 θ ) + ( θ → 0 + lim 2 θ 3 2 sin 2 θ ( 1 − cos θ ) )
θ → 0 + lim θ 3 S = 2 1 + 4 1 + 0
θ → 0 + lim θ 3 S = 4 3
Each limit can be solved in more than one way. I have left out these evaluations.
Set up coordinates with A at the origin and B on the x − axis. Then the coordinates of the points are A ( 0 , 0 ) , B ( sin θ , 0 ) , C ( sin θ , 1 ) , D ( 0 , 1 ) and E ( cos θ ⋅ sin θ , sin 2 θ ) .
The area of A B C E is the sum of the areas of A B E and B C E ; that is S ( θ ) = 2 1 sin 3 θ + 2 1 ( sin θ − cos θ ⋅ sin θ )
Using the small angle approximations sin θ ≈ θ and cos θ ≈ 1 − 2 1 θ 2 , this becomes S ( θ ) ≈ 2 1 θ 3 + 2 1 ( θ − θ + 2 1 θ 3 ) = 4 3 θ 3
Hence the required limit is 4 3 .