Limit and Geometry 003
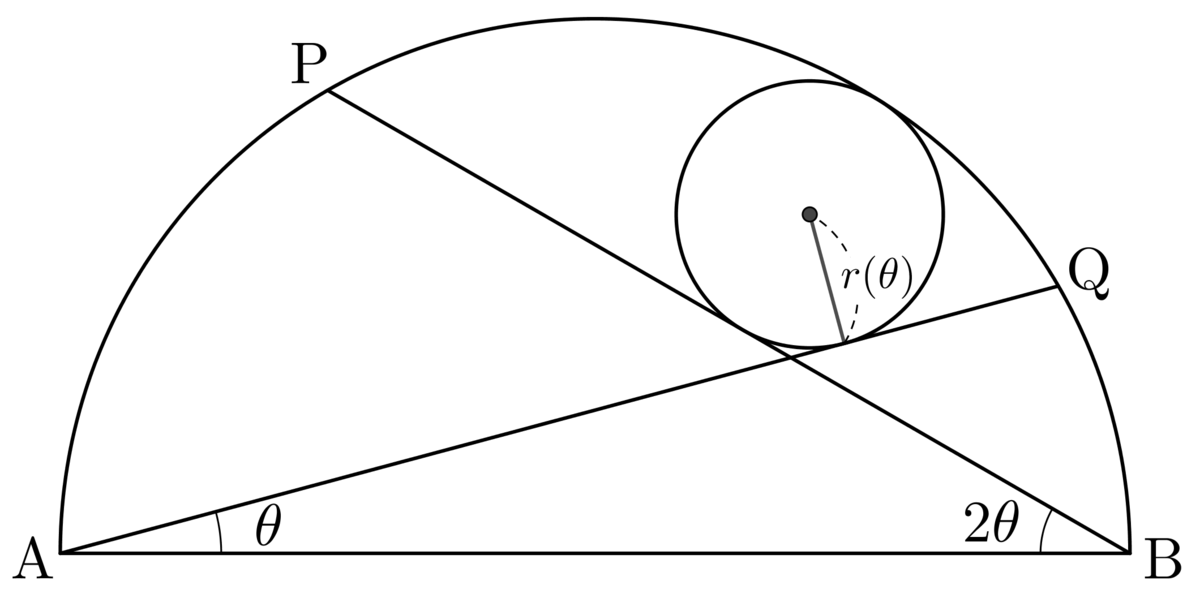
There is a semicircle A B of diameter 2 as shown in the diagram. Let P and Q be the points on arc A B that satisfy ∠ A B P = 2 θ and ∠ B A Q = θ respectively. Let r ( θ ) be the radius of the circle that is tangent to both line segments A Q and B P , and also internally tangent to the arc of the semicircle.
Given that θ → 6 π − lim 6 π − θ r ( θ ) = p 3 + q , where p and q are rational numbers, what is the value of 4 ( p 2 + q 2 ) ?
Bonus : Can you evaluate the limit without using L'Hôpital's rule ?
The answer is 18.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let's choose our coordinate system such that its origin is at the midpoint of A B . At the point where the small circle is tangent to the big semi-circle, the normal passes through the center of the small circle and the center of the big semi-circle, which is the origin. Therefore, we can express the coordinates of the center of the small circle as follows:
C = ( 1 − r ) ( cos ϕ , sin ϕ )
To determine r and ϕ , we use the fact that the distance between C and the two line segments A Q and B P is the radius r .
Now the unit normal vector to A Q that is pointing to point C , is ( − sin θ , cos θ ) , hence,
r = − sin θ ( ( 1 − r ) cos ϕ + 1 ) + cos θ ( 1 − r ) sin ϕ ( 1 )
Similarly, the unit normal vector to B P that is pointing to point C , is ( sin 2 θ , cos 2 θ ) , hence,
r = sin 2 θ ( ( 1 − r ) cos ϕ − 1 ) + cos 2 θ ( 1 − r ) sin ϕ ( 2 )
Equations ( 1 ) , ( 2 ) are linear equations in cos ϕ and sin ϕ . If we define the vector u = ( cos ϕ , sin ϕ ) , then equations ( 1 ) , ( 2 ) can be written compactly as A u = b , where
A = ( 1 − r ) [ − sin θ sin 2 θ cos θ cos 2 θ ]
And,
b = [ r + sin θ r + sin 2 θ ]
The vector u = A − 1 b , and since cos 2 ϕ + sin 2 ϕ = 1 , then b T A − T A − 1 b = 1
Matrix A is a 2 × 2 matrix that is easy to invert.
A − 1 = ( 1 − r ) sin 3 θ − 1 [ cos 2 θ − sin 2 θ − cos θ − sin θ ]
Hence,
A − T A − 1 = ( 1 − r ) 2 sin 2 3 θ 1 [ 1 − cos 3 θ − cos 3 θ 1 ]
and therefore,
b T A − T A − 1 b = ( 1 − r ) 2 sin 2 3 θ 1 ( ( r + sin θ ) 2 + ( r + sin 2 θ ) 2 − 2 cos 3 θ ( r + sin θ ) ( r + sin 2 θ ) ) = 1
from which,
( r + sin θ ) 2 + ( r + sin 2 θ ) 2 − 2 cos 3 θ ( r + sin θ ) ( r + sin 2 θ ) = ( 1 − r ) 2 sin 2 3 θ ( 3 )
Now we have r has a function of θ defined implicity by the above equation, which is just a quadratic in r .
Taking the limit as θ → 6 π , we can see that the limiting r is given by,
( r + 2 1 ) 2 + ( r + 2 3 ) 2 = ( 1 − r ) 2
whose only solution is r = 0 . At this point I used L'Hopital's rule to find the required limit, because we have a 0 0 case, and the required limit will be − θ → 6 π − lim d θ d r .
Differentiating equation ( 3 ) implicitly,
2 ( r + sin θ ) ( r ′ + cos θ ) + 2 ( r + sin 2 θ ) ( r ′ + 2 cos 2 θ ) + 6 sin 3 θ ( r + sin θ ) ( r + sin 2 θ ) − 2 cos 3 θ ( r ′ + cos θ ) ( r + sin 2 θ ) − 2 cos 3 θ ( r + sin θ ) ( r ′ + 2 cos 2 θ ) = 2 ( 1 − r ) ( − r ′ ) sin 2 3 θ + 6 ( 1 − r ) 2 sin 3 θ cos 3 θ
setting θ = 6 π , r = 0 , we get,
( r ′ + 2 3 ) + 2 ( 2 3 ) ( r ′ + 1 ) + 6 ( 4 3 ) = − 2 r ′
so that,
r ′ ( 3 + 3 ) = − 3 3
r ′ = ( 3 + 3 ) − 3 3 = − 6 ( 9 3 − 9 ) = − 2 3 3 + 2 3
Therefore, the required limit is − r ′ = 2 3 3 − 2 3 , so that p = 2 3 and q = − 2 3 , and thus 4 ( p 2 + q 2 ) = 1 8
Let the intersection point of lines A Q and B P be T . Near the limit, the arc of the semicircle joining P and Q can be approximated by a straight line, so that r is approximately the inradius of the triangle Δ P T Q . Even better, this triangle is very nearly right-angled (which makes calculating r easier).
Applying the sine rule in Δ A T B , we have sin 3 θ A B = sin 2 θ A T = sin θ B T
so that A T = sin 3 θ 2 sin 2 θ , B T = sin 3 θ 2 sin θ
If we let the midpoint of A B be O , then the triangles Δ A O Q and Δ B O P are isosceles and we find A Q = 2 cos θ , B P = 2 cos 2 θ
Putting these together, Q T = 2 cos θ − sin 3 θ 2 sin 2 θ , P T = 2 cos 2 θ − sin 3 θ 2 sin θ
Finally, it's also easy to show that P Q = 2 cos 3 θ .
These hold for any θ . However, we're interested in the limit as θ → 6 π − ; so let θ = 6 π − ε , where ε is small and positive.
Now, in a right-angled triangle with legs a , b and hypotenuse c , the inradius is given by 2 a + b − c . Since Δ P T Q is very close to being a right-angled triangle, the quantity we want to find is ε → 0 lim 2 ε P T + Q T − P Q = ε → 0 lim 2 ε 2 cos 2 θ − sin 3 θ 2 sin θ + 2 cos θ − sin 3 θ 2 sin 2 θ − 2 cos 3 θ = ε → 0 lim ε sin 3 θ sin 3 θ ⋅ cos 2 θ − sin θ + sin 3 θ ⋅ cos θ − sin 2 θ − sin 3 θ ⋅ cos 3 θ
Although ε is small, θ is not, so we have to be a little careful with small angle substitutions. The easiest way to avoid problems is to expand the trig functions; for example, 3 θ = 2 π − 3 ε so that sin 3 θ = cos 3 ε and so on.
Using the small-angle substitutions cos ε = 1 − 2 1 ε 2 + O ( ε 4 ) and sin ε = ε + O ( ε 3 ) and dropping terms of O ( ε 3 ) and above, the limit becomes
ε → 0 lim ε cos 3 ε cos 3 ε ⋅ cos ( 3 π − 2 ε ) − sin ( 6 π − ε ) + cos 3 ε ⋅ cos ( 6 π − ε ) − sin ( 3 π − 2 ε ) − sin 3 ε ⋅ cos 3 ε = ε → 0 lim ε 2 3 ( 3 − 1 ) ε − 2 3 ( 3 + 2 ) ε 2 = 2 3 ( 3 − 1 )
so p = 2 3 , q = − 2 3 and the answer is 1 8 .