This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
x → 0 + lim x x = e ( l i m x → o + 1 / x lo g x ) = 1
(As l i m x → o + x 1 lo g x = 0 , by applying L'Hôpital's rule )
⇒ I = n → ∞ lim n 3 ∑ r = 1 n ⌊ r 2 ⌋
⇒ I = n → ∞ lim r = 0 ∑ n ( n r ) 2 n 1
⇒ I = ∫ 0 1 t 2 d t
(Integral as limit of Riemann Sum)
⇒ I = 3 t 3 ∣ ∣ ∣ 0 1 = 1 / 3
⇒ ⌊ 1 0 0 0 I ⌋ = 3 3 3
Hi, you can use \infty instead of inf to represent infinity :)
Log in to reply
Oops! My bad... ;). I put '\inf' instead of '\infty'. Thanks for pointing it out. I'll go ahead and edit that.
You cannot just interchange limits without justification.
Log in to reply
Yes, i had some doubts about that too. Could you (or anyone) help me justify it? Or is it just incorrect?
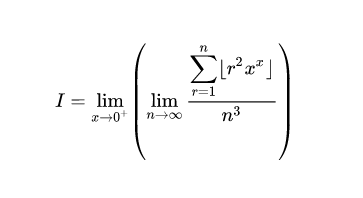
⌊ x ⌋ = x − { x }
I = x → 0 + lim ( n → ∞ lim n 3 ∑ r = 1 n r 2 × x x − n 3 ∑ r = 1 n { r 2 × x x } )
n → ∞ lim n 3 ∑ r = 1 n r 2 × x x = 6 n 3 n ( n + 1 ) ( 2 n + 1 ) = n → ∞ lim 6 ( 1 + n 1 ) ( 2 + n 1 ) = 3 1
N o w , 0 ≤ { r 2 × x x } < 1
n → ∞ lim n 3 ∑ r = 1 n { r 2 × x x } = 0
Thus , I = lim x → 0 + 3 x x
lim x → 0 + x x = e x l o g x = e lim x → 0 + x l o g x = lim x → 0 + e x 1 = 1 ( as it forms ∞ ∞ so we can apply L.H )
⌊ 3 1 0 0 0 ⌋ = ⌊ 3 3 3 . 3 3 3 ⌋ = 3 3 3