Limit for you

Relevant wiki: Riemann Sums

$\begin{aligned} S & = \lim_{n \to \infty} \sum_{k=1}^n \frac 4n \sqrt{\frac {2k}n-\frac {k^2}{n^2}} & \small \color{#3D99F6} \text{By Riemann sum }\lim_{n \to \infty} \frac 1n \sum_{k=a}^b f \left(\frac kn \right) = \lim_{n \to \infty} \int_\frac an^\frac bn f(x) \ dx \\ & = 4\int_0^1 \sqrt {2x-x^2} dx & \small \color{#3D99F6} \text{Using identity }\int_a^b f(x) \ dx = \int_a^b f(a+b-x) \ dx \\ & = 4\int_0^1 \sqrt {\color{#3D99F6}1-x^2} dx & \small \color{#3D99F6} \text{Let }x = \sin \theta \implies dx = \cos \theta \ d\theta \\ & = 4 \int_0^\frac \pi 2 \cos^2 \theta \ d\theta & \small \color{#3D99F6} \text{Note that }\cos 2\theta = 2\cos^2 \theta - 1 \\ & = 4 \int_0^\frac \pi 2 \frac {1+\cos (2\theta)}2 \ d\theta \\ & = 2 \left[\theta + \frac {\sin (2\theta)}2 \right]_0^\frac \pi 2 \\ & = \pi \approx \boxed{3.142} \end{aligned}$

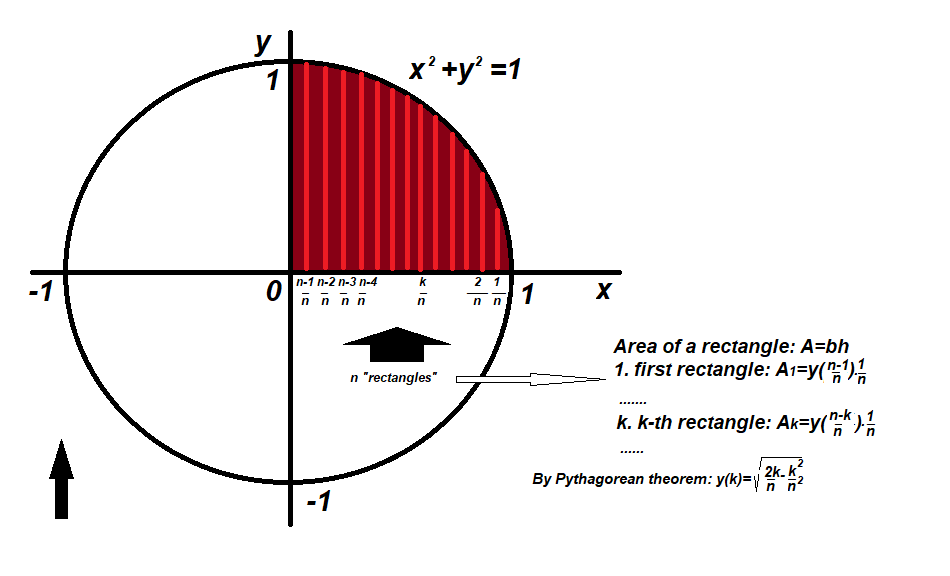
This is maybe not a rigorous solution, but this is how i came up with this question. Let's look at the circle with radius 1, and centered at (0,0). It's equation is: $\ x^{2}+y^{2}=1$ Its area is $\ A=\pi$ Now let's find its area in another way. We can compute the area with integral: $\ A= 4 \int_0^1 \sqrt{1-x^{2}} dx=4 \frac{\pi}{4} = \pi$ Now, the sigma notation and limit in the question remind of the defintion of the definite integral: $\ \int_a^b f(x) dx = \lim_{n \to \infty} \sum_{k=1}^n (\frac{(b-a)}{n} f(a+\frac{kb}{n}))$ And we can factor out the constant: $\ \int_a^b f(x) dx = \lim_{n \to \infty} \frac{(b-a)}{n} \sum_{k=1}^n f(a+\frac{kb}{n})$ In our case: $\ a=0$ $\ b=1$ And: $\ f(x)=\sqrt{1-\frac{k^{2}}{n^{2}}}$ Now if we substitute $\ k_0=n-k$ ,(we are counting from right (1) to left (0)), we get: $\ \int_a^b f(x) dx = \lim_{n \to \infty} \frac{(1)}{n} \sum_{k_0=1}^n \sqrt{1-\frac{n^{2}-2k_0n+k_0^{2}}{n^{2}}}$ $\ \frac{\pi}{4} = \int_a^b f(x) dx = \lim_{n \to \infty} \frac{1}{n} \sum_{k_0=1}^n \sqrt{\frac{2k_0}{n}-\frac{k_0^{2}}{n^{2}}}$ This is equivalent with: $\ \lim_{n \to \infty} \sum_{k=1}^n \frac{4}{n} \sqrt{\frac{2k}{n}-\frac{k^{2}}{n^{2}}} =\boxed{\pi}$