Limit-forbidden zone - Part 1

Calculus Level 3

One day, Alice encountered this problem on an exam:

Given that $f(x)=(x-1)e^x+a x^2$ , if $f(x)=0$ has exactly two roots, then find the range of $a$ and prove it.

By using the derivative and its graph, Alice quickly reach the conclusion that $a>0$ .

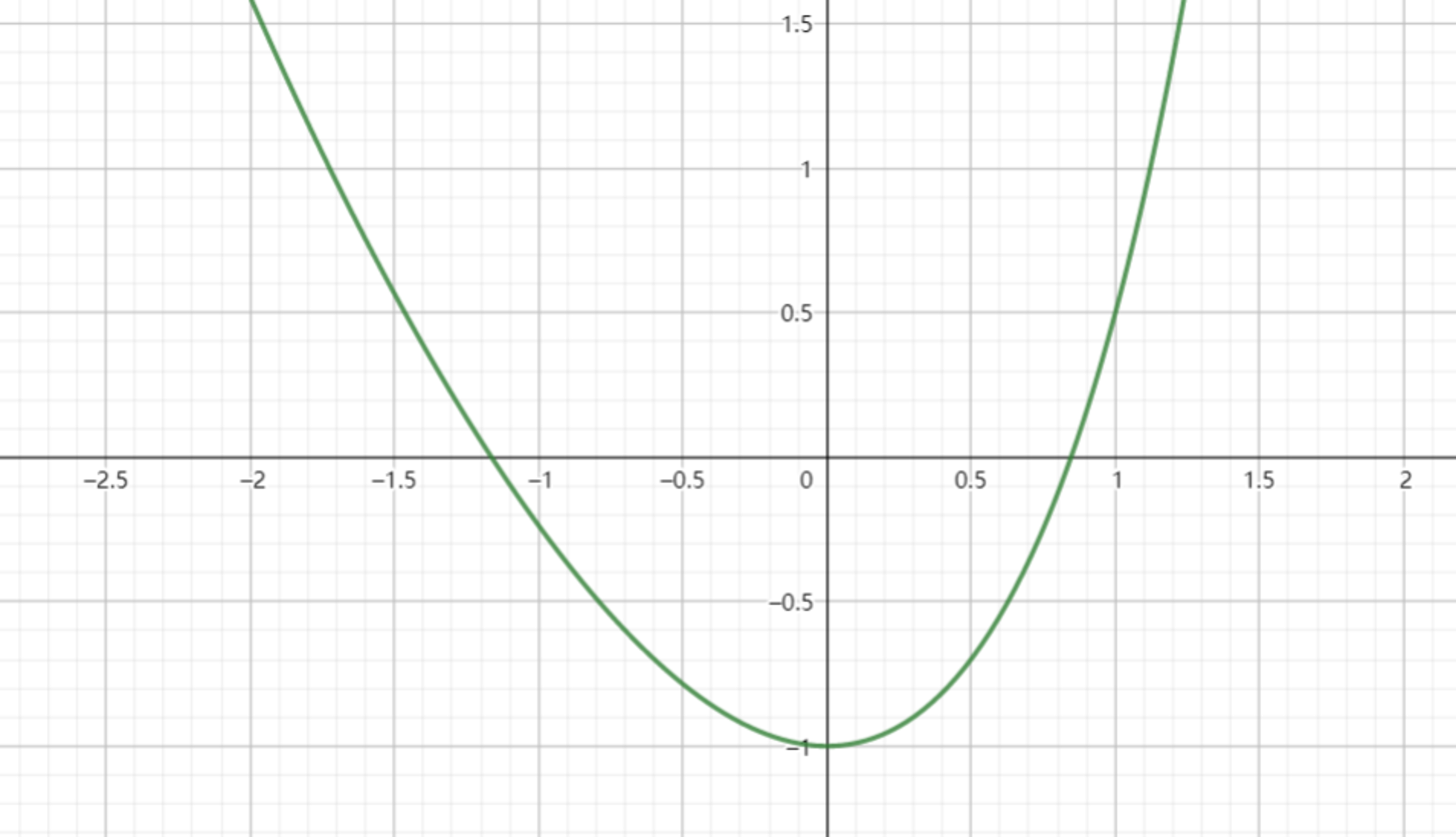
But one thing troubled her greatly: Since she is a high school student and it's a standard exam, she is not permitted to use any definition of limit to prove the existence of roots.

"What a joke," she thought, but she quickly calmed down and came up with an idea: "You are not letting me use any definition of limit, but what I am really doing is using a simpler version of Epsilon-Delta Definition . If I could prove that for all $a>0$ , I can always find $\delta \in \mathbb R$ such that $f(\delta)>0$ , then I can prove the existence of roots by Intermediate Value Theorem."

For the positive root, she quickly tried $\delta=1$ and $f(\delta)=a>0$ , and she was very delighted.

For the negative root, she thought for a minute and decided to try $\delta=-a^n$ , where $n$ is a constant. Now she was having trouble deciding what $n$ to choose.

Can you help her choose a proper $n$ , so that for all $a>0$ , $f(\delta)>0$ ?

n=\dfrac{1}{2}

n=2

n=1

n=-1

n=-2

n=-\dfrac{1}{2}

1 solution

Shikhar Srivastava
Apr 16, 2020

We have $\delta = -a^n$

So that $f(\delta) = (-a^n - 1)e^{-a^n} + a(-a^n)^2$

$\hspace{50pt} = -(a^n + 1)e^{-a^n} + a^{2n+1}$

Now finding the value of n so that $f(\delta) > 0$ for all $a > 0$

$-(a^n + 1)e^{-a^n} + a^{2n+1} > 0$

$\Rightarrow a^{2n+1} > (a^n + 1)e^{-a^n}$

Both LHS and RHS are positive for any $a > 0$ and any $n$ . So taking natural logarithm on both side.

$(2n+1)\text{log }a > \text{log}(a^n + 1) - a^n \hspace{20pt}\cdots \text{Eq. 1}$

Now considering RHS.

Let $g(x) = \text{log}(1 + x) - x$

$\Rightarrow g'(x) = \Large\frac{1}{1 + x}$ $- 1 = \Large\frac{- x}{1 + x}$

We see that $g'(x) = 0$ at $x = 0$ and $g'(x) < 0$ for all $x >0$ . Also, $g(0) = 0$

All these implies that $g(x) < 0$ for all $x > 0$ .

For any $a > 0\,,\,a^n > 0$ . So because of above argument, $\text{log}(a^n + 1) - a^n < 0$ for all $a > 0$ .

For $\text{Eq. 1}$ to be true we have to choose $n$ so that

$(2n+1)\text{log }a \geq 0$ for all $a > 0$

$\text{log }a$ can take any real value for $a > 0$ . So the above inequation can only be true when coefficient of $\text{log }a$ is $0$ .

$2n + 1 = 0\newline\Rightarrow n = -\Large\frac{1}{2}$

Limit-forbidden zone - Part 1

1 solution

0 pending reports