Limit of a Definite Integral 3
n → ∞ lim ∫ 0 n π e − x ∣ sin ( x ) ∣ d x
If the limit above can be expressed as α ( 1 − e λ 1 + e β ) where α , β , λ are real numbers, α ≥ 0 and β , λ ≤ 0 and n is an integer, find the value of 2 ( α + β − λ ) .
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
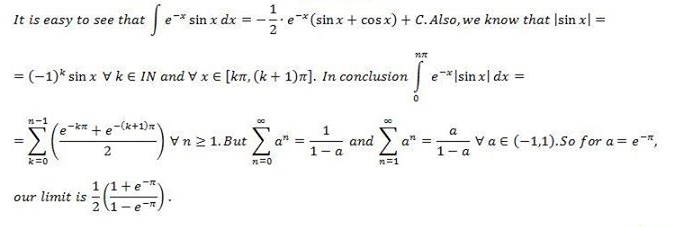
Edit the question because,
2 1 ( 1 − e − π ) ( 1 + e − π ) = 2 − 1 ( 1 − e π ) ( 1 + e π )
Log in to reply
Thanks for informing me. I never noticed it :/