Limit of a Sequence 001
Let n be a positive integer. Compute the limit
n → ∞ lim cos ( π 4 n 2 + 5 n + 1 )
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Yes, same method, but one thing bugs me, that is as n is approaching infinity, can we say that n will be an integer? I mean, we can take large integers for the limit, but in the question it's not mentioned explicitly that n is an integer, so will things really workout the way we want?
Here is a similar proof:
Note that for any integer n, cos(2npi+x)=cosx
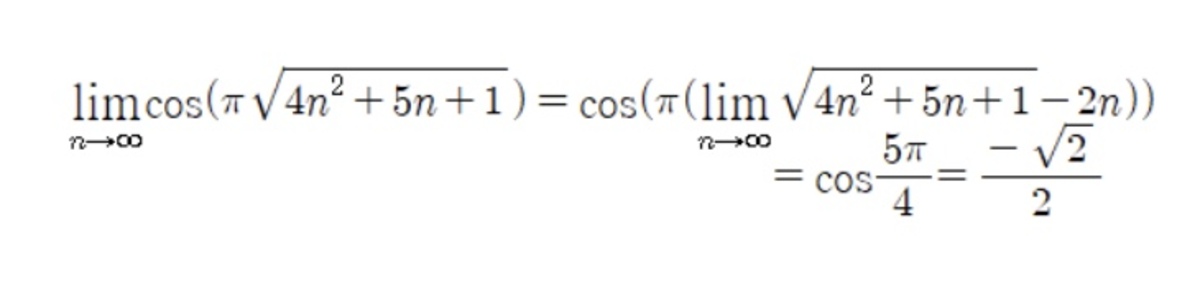
This comment was made before O.P. solved the problem totally. Note that for any integer n, c o s x = c o s ( 2 n π + x ) . Also note that 4 n 2 + 5 n + 1 − 2 n goes to 4 5 as n goes to infinity. c o s ( π 4 n 2 + 5 n + 1 ) = c o s ( π 4 n 2 + 5 n + 1 − 2 n ) )
Since cosx is a continuous function the value that we are looking for is cos(5π/4) hence -1/sqrt2
Consider the expression:
N = 4 n 2 + 5 n + 1
N = 2 n 1 + 4 n 5 + 4 n 2 1
If n is a very large integer, then the terms 4 n 5 and 4 n 2 1 are very small. This allows us to approximate N as follows:
N = 2 n ( 1 + 4 n 5 + 4 n 2 1 ) 1 / 2
N ≈ 2 n ( 1 + 2 1 ( 4 n 5 + 4 n 2 1 ) ) ⟹ N ≈ 2 n + 4 5 + 4 n 1
The above is a first-degree binomial approximation of the expression. Now, the cosine can also be approximated as such:
cos ( π N ) = cos ( 2 π n + 4 5 π + 4 n π )
Since n is large, then 4 n π can be neglected. Then:
cos ( π N ) = cos ( 2 π n + 4 5 π )
Since n is an integer:
cos ( π N ) = cos ( 2 π n + 4 5 π ) = cos ( 4 5 π ) = − 2 1