Limit with Sphere
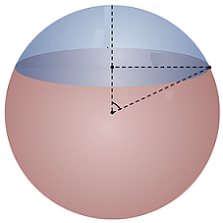
In a unit ball, the area of cross-section in a plane and the curved surface area of corresponding minor spherical cap are denoted by a and A ( a ) respectively.
Evaluate a → 0 lim a 2 A ( a ) − a .
The answer is 0.07957747.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
There is probably a more elegant solution, but here is mine:
Let r be the horizontal radius of the spherical cap, which itself has a height of h , so the distance from the center of the sphere and the horizontal plane of the spherical cap is 1 − h . Before proceeding with the solution, first note that the area of the horizontal plane of the spherical cap is a = π r 2 and the surface area of the spherical cap itself is given by A = π ( r 2 + h 2 ) or A = a + π h 2
The following relationship holds: r 2 + ( 1 − h ) 2 = 1 Or when expanded: r 2 + h 2 + 1 − 2 h = 1 Multiplying both sides by h and rearranging a bit yields: π ( r 2 + h 2 ) = 2 π h Notice that the left hand side is precisely A , so: A = 2 π h or h = 2 π A h 2 = 4 π 2 A 2 I squared both sides because now we can plug into the equation A = a + π h 2 : A = a + π 4 π 2 A 2 Rearranging again we get this quadratic equation in terms of A: A 2 − 4 π A + 4 π a = 0 Using quadratic formula or completing the square yields: ( A − 2 π ) 2 = 4 π ( π − a ) A = 2 π ± 2 π ( π − a ) We get two possible solutions for A ( a ) but clearly, the one of interest is with the negative sign since, by corollary, if a → 0 then so must A . Therefore: A ( a ) = 2 π − 2 π ( π − a ) Now we found A in terms of a we can evaluate the limit: a → 0 lim a 2 A ( a ) − a a → 0 lim a 2 2 π − 2 π ( π − a ) − a From here on, multiple cases of undeterminate forms 0 " 0 " emerge so applying L'Hopital's rule twice will finally yield: a → 0 lim 4 π ( π − a ) − 3 / 2 = 4 π 1 ≈ 0 . 0 7 9 6
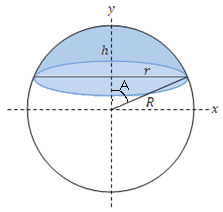
From the above figure we have, r = R sin A = sin A since R = 1 ⟹ area of cross-section, a = π ∗ r 2 = π sin 2 A
h = R − R cos A = 1 − cos A . Curved surface area of minor cap is, A ( a ) = 2 π h R = 2 π ( 1 − cos A )
Now, lim a → 0 a 2 A ( a ) − a = lim A → 0 ( π sin 2 A ) 2 2 π ( 1 − cos A ) − π sin 2 A [since a = π sin 2 A , a → 0 ⟹ A → 0 ]
= π 1 × lim A → 0 sin 4 A 4 sin 2 ( 2 A ) − 4 sin 2 ( 2 A ) cos 2 ( 2 A ) = π 1 × lim A → 0 sin 4 A 4 sin 2 ( 2 A ) ( 1 − cos 2 ( 2 A ) )
= π 4 × lim A → 0 sin 4 A sin 4 ( 2 A ) = π 4 × lim A → 0 2 4 2 4 A 4 sin 4 A A 4 sin 4 ( 2 A ) = π 4 × 2 4 1 = 4 π 1 ≈ 0 . 0 7 9 5
Let r and h be the radius of the base and the height of the spherical cap, respectively. Then from the right triangle shown in the diagram in the question, we get
r 2 = 1 2 − ( 1 − h ) 2 = 2 h − h 2
The area of a spherical cap is given by 2 π R h , where R is the radius of the sphere; in our case we have R = 1 , so A ( a ) = 2 π h . Also, a = π r 2 = π ( 2 h − h 2 ) .
Then, since as a → 0 we have h → 0 , we get
lim a → 0 a 2 A ( a ) − a = lim h → 0 π 2 ( 2 h − h 2 ) 2 2 π h − π ( 2 h − h 2 ) = lim h → 0 π 2 h 2 ( 2 − h ) 2 π h 2 = lim h → 0 π ( 2 − h ) 2 1 = 4 π 1 ≈ 0 . 0 7 9 5 7 7 4 7