Limited Factors
Find the number of positive integers less than 1 0 0 0 that evenly divide
2 2 0 − 1
The answer is 23.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
The question previously did not explicitly state positive integers. Those who answered 71 ( 23 positive, 48 negative ) were marked correct.
Is there a faster way of doing this problem? I got the DoS part..
Log in to reply
I would like to know the answer to this as well. But I think that my solution is the fastest.
I'm confused on whether I should use programming or not to solve such problems.
2 1 0 + 1 is sophie germainable :3
Did the same way !
Seeing no clever way of doing this I used the Python sympy library:

Using Java Netbeans Programmer..
This Is the Programming screen
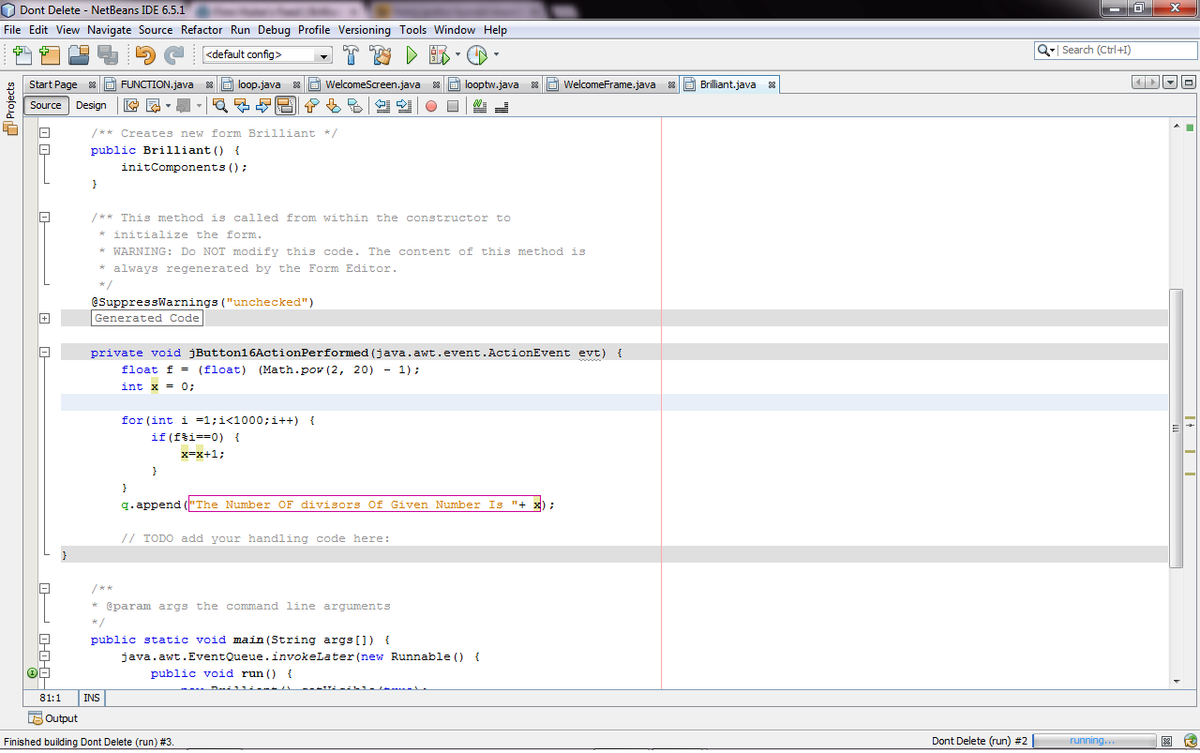
Output Screen
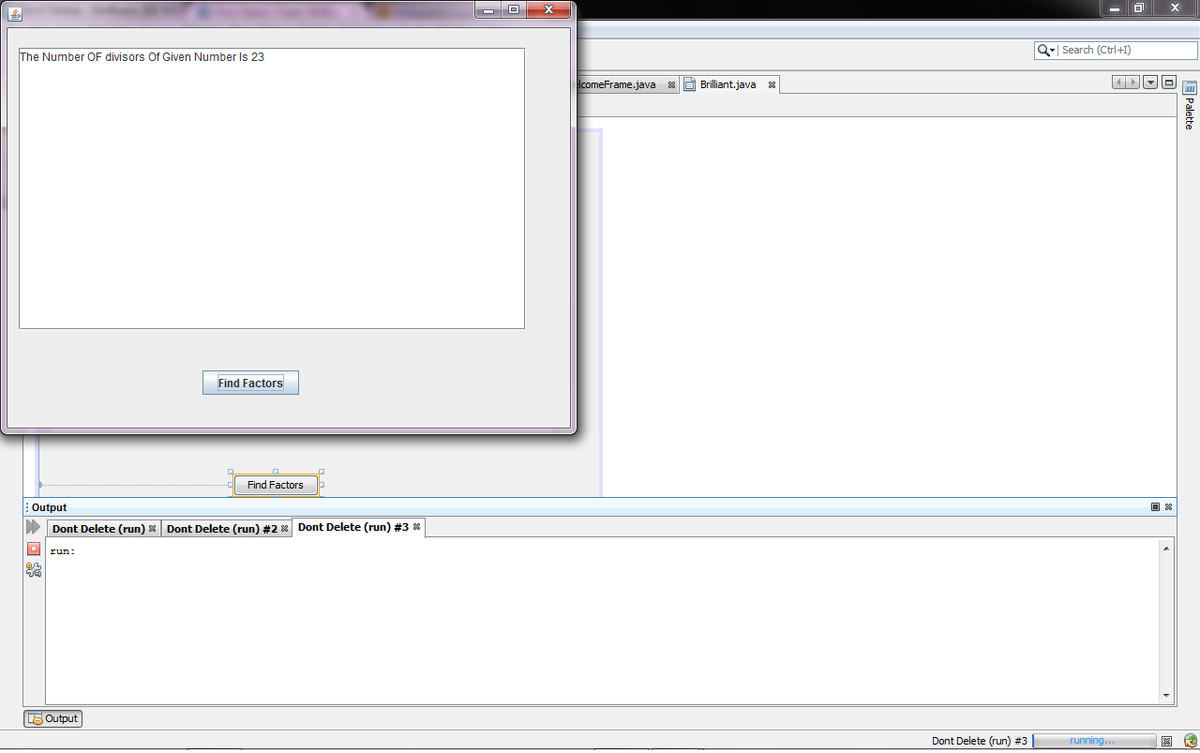
And Output Is 23..
Haha, that is the efficient method. Why waste your time factoring when you can script in a minute ;)
Here is my solution:
2 2 0 − 1 = 1 0 4 8 5 7 5 = ( 3 ) ( 5 2 ) ( 1 1 ) ( 3 1 ) ( 4 1 )
Now we can count the number of factors from the prime factorization, but we must remember: our factors must be less than 1000. Generating our factors less than 1000, we have:
1 , 3 , 5 , 1 1 , 1 5 , 2 5 , 3 1 , 3 3 , 4 1 , 5 5 , 7 5 , 9 3 , 1 2 3 , 1 5 5 , 1 6 5 , 2 0 5 , 2 7 5 , 3 4 1 , 4 5 1 , 4 6 5 , 6 1 5 , 7 7 5 , 8 2 5
Java solution -
int n = 0;
for(int i = 1; i < 1000; i++)
if((Math.pow(2,20) - 1) % i == 0) n++;
System.out.println(n);
Same Here!!
1, 3, 5, 11, 15, 25, 31, 33, 41, 55, 75, 93, 123, 155, 165, 205, 275, 341, 451, 465, 615, 775, 825 -- in all 23 factors.
Factoring by DoS gives ( 2 1 0 − 1 ) ( 2 1 0 + 1 ) . Further expanding, ( 2 5 − 1 ) ( 2 5 + 1 ) ( 2 1 0 + 1 ) . We can compute this quickly to get 2 2 0 − 1 = ( 3 1 ) ( 3 3 ) ( 1 0 2 5 ) . Luckily for us, 3 1 × 3 3 > 1 0 0 0 , and 1 0 2 5 > 1 0 0 0 , which knocks out a lot of difficult casework. Factoring the entire thing gives
3 × 5 2 × 1 1 × 3 1 × 4 1 .
The tricky part is counting. We can isolate factors and construct a list. Factors that are divisible by 3 : 3 , 1 5 , 3 3 , 7 5 , 9 3 , 1 2 3 , 1 6 5 , 4 6 5 , 6 1 5 , 8 2 5 . Factors divisible by 5 that aren't already accounted for: 5 , 2 5 , 5 5 , 1 5 5 , 2 0 5 , 2 7 5 , 7 7 5 . Factors divisible by 1 1 that aren't already accounted for: 1 1 , 3 4 1 , 4 5 1 . Last but not least, we have just 1 , 3 1 , and 4 1 . Thus, there are 2 3 integers less than 1 0 0 0 that divide 2 2 0 − 1 .