Limiting behavior of the area of an infinity-gon

The area of the n-gon can be found by dividing it into N isosceles triangles constructed from two consecutive n-gon vertices plus the central point of the n-gon, as shown here for a 12-gon: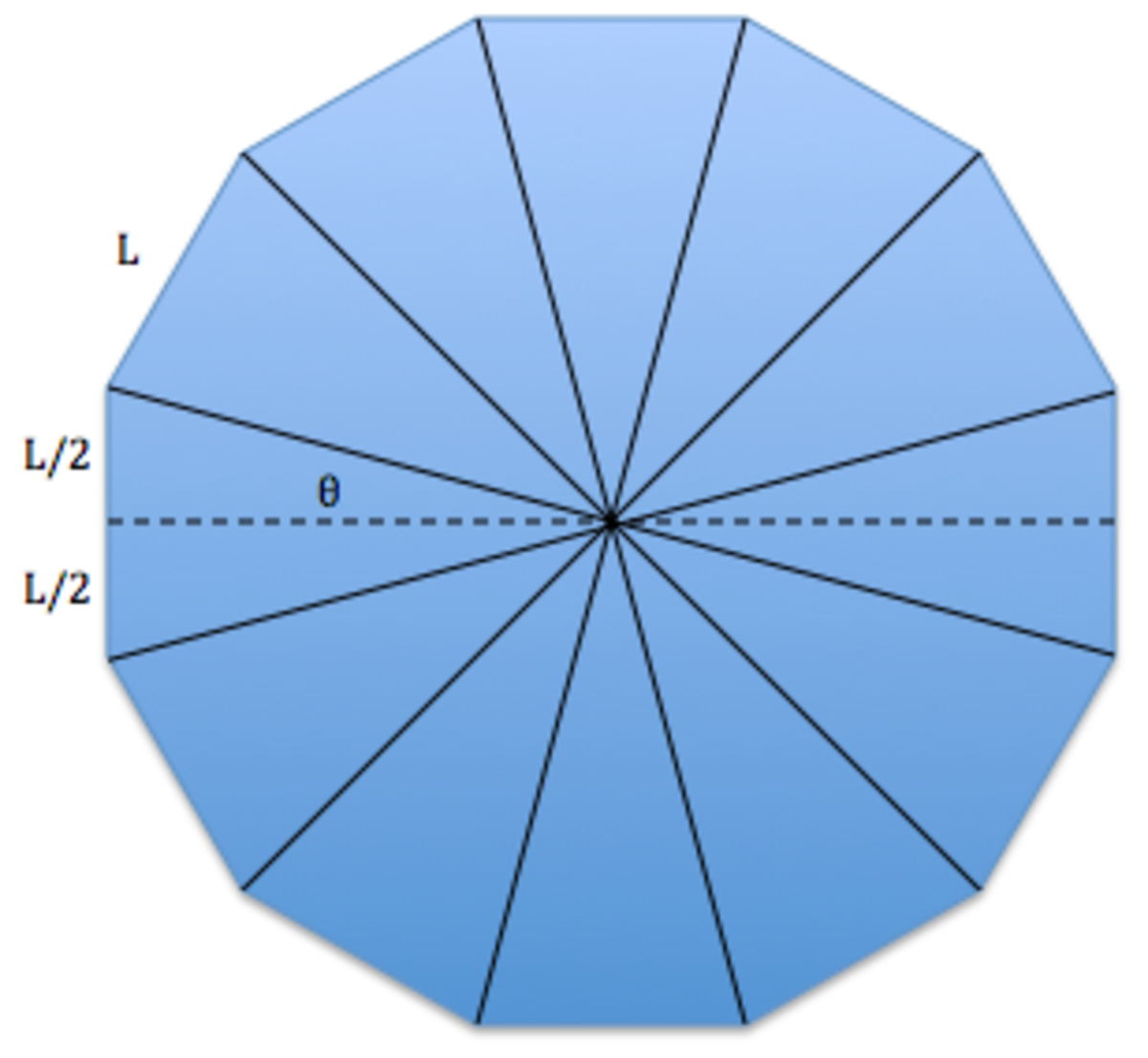

Each of our N isosceles triangles has an area that can be found by dividing in half, forming two identical right triangles, as shown in the diagram. The angle marked $\theta$ on the diagram is $\pi/N$ .

The area of one of the right triangles is $\frac{L^2}{8\tan(\pi/N)}$ . The area of one of the isosceles triangles is twice that, so the area of the whole n-gon is

$A(N) = \frac{N L^2}{4 \tan(\pi/N)}$

$A(N) = \frac{N L^2}{4} \cot(\pi/N)$

Our goal is to find the limiting behavior $\lim_{N \to \infty} A(N)$ . The Taylor series expansion of $\cot(x)$ is

$\cot(x) = \frac 1 x - \frac 1 3 x + O(x^3)$

Therefore

$A(N) = \frac{N L^2}{4} (\frac{N}{\pi} - \frac{\pi}{3 N} + O(N^{-3}))$

$A(N) = \frac{N^2 L^2}{4 \pi} - \frac{L^2 \pi}{12} + O(N^{-2}))$

And in the limit $N \to \infty$ ,

$A(N) \sim \frac{N^2 L^2}{4 \pi}$

If we evaluate this with $L = 2 \sqrt{\pi}$ , we find that

$A(N) \sim N^2$