Limiting Problem
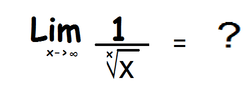What is the limit of the function as "x" approaches infinity ?
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
↪
I
n
c
o
m
p
l
e
t
e
S
o
l
u
t
i
o
n
How did you directly evaluate
∞
0
as
∞
0
is an
i
n
d
e
t
e
r
m
i
n
a
t
e
f
o
r
m
Observe that this is equivalent to lim x → ∞ x x lim x → ∞ 1 . We know that x x = x 1 / x = e x ln x . Since, ln x grows slower than x , x x = 1 as x goes to infinity. Hence, the original limit goes to 1 as well.
Another possible way to evaluate this is rewriting the limit using the substitution m = x 1 as, m → 0 lim ( m m ) If you evaluate it now, the value comes out as 0 0 which is taken as 1 most of the time but that isn't true for all cases and the value is undefined! Checking the limit by substituting values of x like x = 0 . 0 0 0 0 1 gives us a result tending to 1 . So, the value of the limit is 1 . This concludes the solution.
This looks to be the most comprehensive one.
x → ∞ lim x x 1 1 = ∞ ∞ 1 1 = ∞ 0 1 = 1 1 = 1