Limits #1
x → ∞ lim ( 2 x 2 + 5 2 x 2 + 3 ) 8 x 2 + 3
If the limit above is equal to e m , where m is an integer, input m .
The answer is -8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Yeah, but this 1^infty method works for all f, g, h functions?
Log in to reply
I am trying to find the proof for it. Any reference?
Log in to reply
If f ( x ) and g ( x ) = 0 are continuous functions in R and g ( x f ( x ) → 1 as x → a this method works.
Old method 1.- x → ∞ lim ( 2 x 2 + 5 2 x 2 + 3 ) 8 x 2 + 3 = x → ∞ lim ( 2 x 2 + 3 2 x 2 + 5 ) − ( 8 x 2 + 3 ) = = x → ∞ lim ( 1 + 2 x 2 + 3 2 ) − ( 8 x 2 + 3 ) = x → ∞ lim ( 1 + 2 2 x 2 + 3 1 ) ( 2 ( 2 x 2 + 3 ) ) ⋅ ( 2 2 x 2 + 3 − ( 8 x 2 + 3 ) ) = e − 8 2.- x → ∞ lim ( 2 x 2 + 5 2 x 2 + 3 ) 8 x 2 + 3 = x → ∞ lim ( 2 x 2 + 3 2 x 2 + 5 ) − ( 8 x 2 + 3 ) = = x → ∞ lim ( 1 + 2 x 2 + 3 2 ) − ( 8 x 2 + 3 ) = e lim x → ∞ − ( 8 x 2 + 3 ) ⋅ 2 x 2 + 3 2 = e − 8 due to ln ( 1 + x ) ∼ x , as x → 0
Thank you very much
Log in to reply
Hey, if you want to show that m belongs to the set of integers, then the following Latex code would be better:
m \in \mathbb{Z}
This will give the output as
m ∈ Z .
Good problem but highly over rated .
Set u = 2 x 2 + 5 . Then the entire limit may be rewritten as u → ∞ lim ( u u − 2 ) 4 u − 1 7 = u → ∞ lim ( 1 − u 2 ) 4 u ⋅ ( 1 − u 2 ) − 1 7 = e − 8 ⋅ 1 − 1 7 = e − 8
Firstly, note that ( 2 x 2 + 5 2 x 2 + 3 ) 3 = ( 2 + 5 / x 2 2 + 3 / x 2 ) 3 → 1 a s n → ∞ ( 1 )
By application of Algebra Of Limits (a.k.a AOL) (quotient rule then product rule). So assuming the given limit exists we have, taking the exponential of the log of the given expression : (and from (1)) x → ∞ lim ( 2 x 2 + 5 2 x 2 + 3 ) 8 x 2 + 3 = x → ∞ lim e x p ( 8 x 2 ( L n ( 2 x 2 + 3 ) − L n ( 2 x 2 + 5 ) ) Letting u = 2 x 2 and using continuity of e x p : ( 0 , ∞ ) → R = u → ∞ lim e x p ( 4 u ( L n ( u + 3 ) − L n ( u + 5 ) ) ) = e x p ( u → ∞ lim ( 4 u ( L n ( u + 3 ) − L n ( u + 5 ) ) ) ) ( 2 ) Now lim u → ∞ ( u + 3 ) ( u + 5 ) u 2 exists and equals 1 (by same method used to obtain (1)) so we can apply L'Hopital's Rule (and AOL) to (2) as follows: = e x p ( 4 u → ∞ lim d u d ( 1 / u ) d u d ( L n ( u + 3 ) − L n ( u + 5 ) ) ) = e x p ( 4 u → ∞ lim − u 2 1 u + 3 1 − u + 5 1 ) = e x p ( − 8 u → ∞ lim ( u + 3 ) ( u + 5 ) u 2 ) = e x p ( − 8 )
(1-1/f(x))^f(x) >>>>>> as f(x) tends infinity, this tends to e^(-1)
Use this as a hint
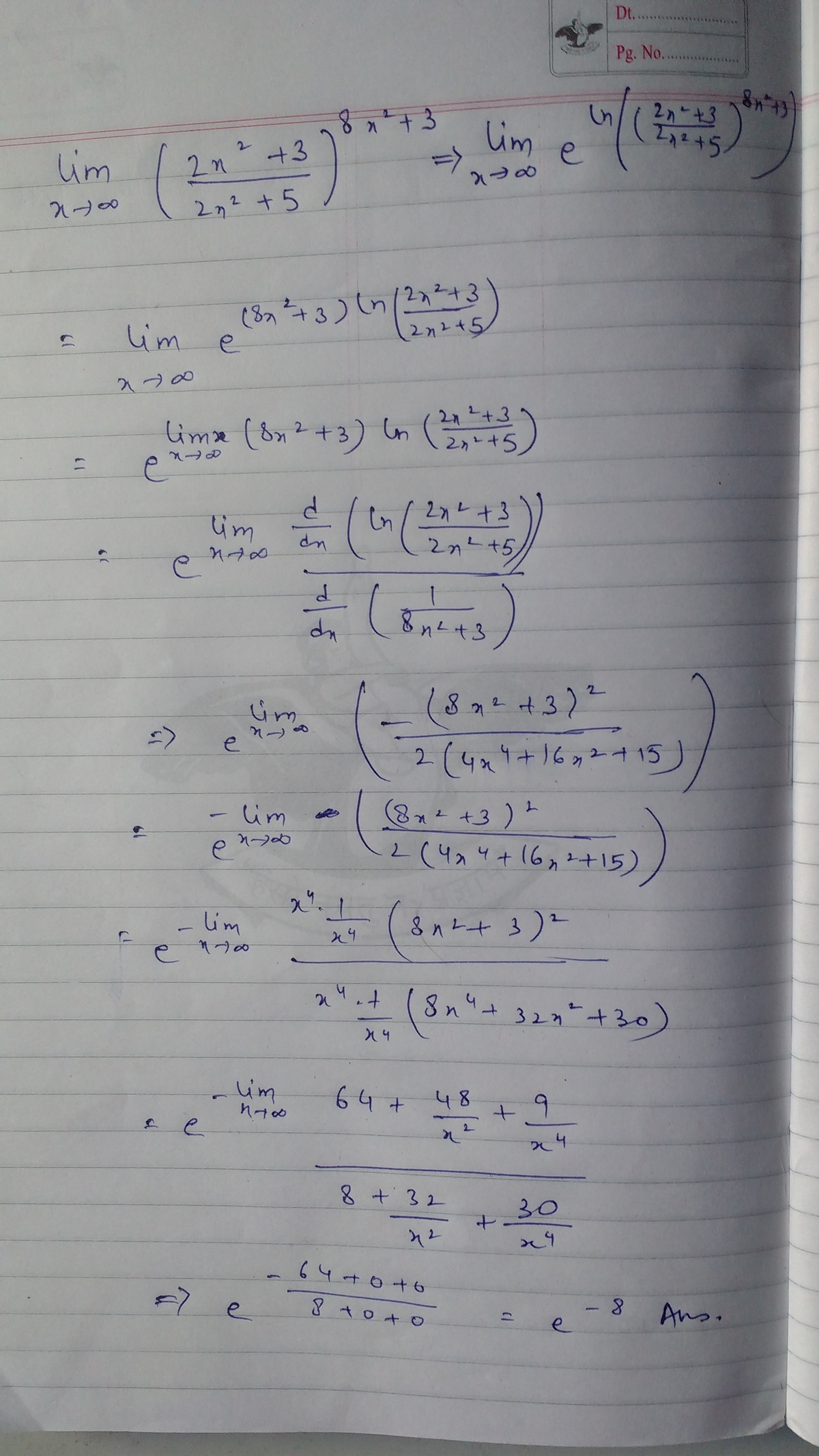

L = x → ∞ lim ( 2 x 2 + 5 2 x 2 + 3 ) 8 x 2 + 3 = exp ( x → ∞ lim ( 8 x 2 + 3 ) ( 2 x 2 + 5 2 x 2 + 3 − 1 ) ) = exp ( x → ∞ lim 2 x 2 + 5 − 2 ( 8 x 2 + 3 ) ) = exp ( x → ∞ lim 2 x 2 + 5 − 1 6 x 2 − 6 ) = e − 8 A 1 ∞ case, see note.
⟹ m = − 8
Note: For lim x → a ( g ( x ) f ( x ) ) h ( x ) = 1 ∞ , we have ( see method 2 ):
lim x → a ( g ( x ) f ( x ) ) h ( x ) = exp ( lim x → a h ( x ) ( g ( x ) f ( x ) − 1 ) )