Limits and Integrals together.
n → ∞ lim n ∫ 0 4 π tan n x d x
Find the limit above.
The answer is 0.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Exactly the same!
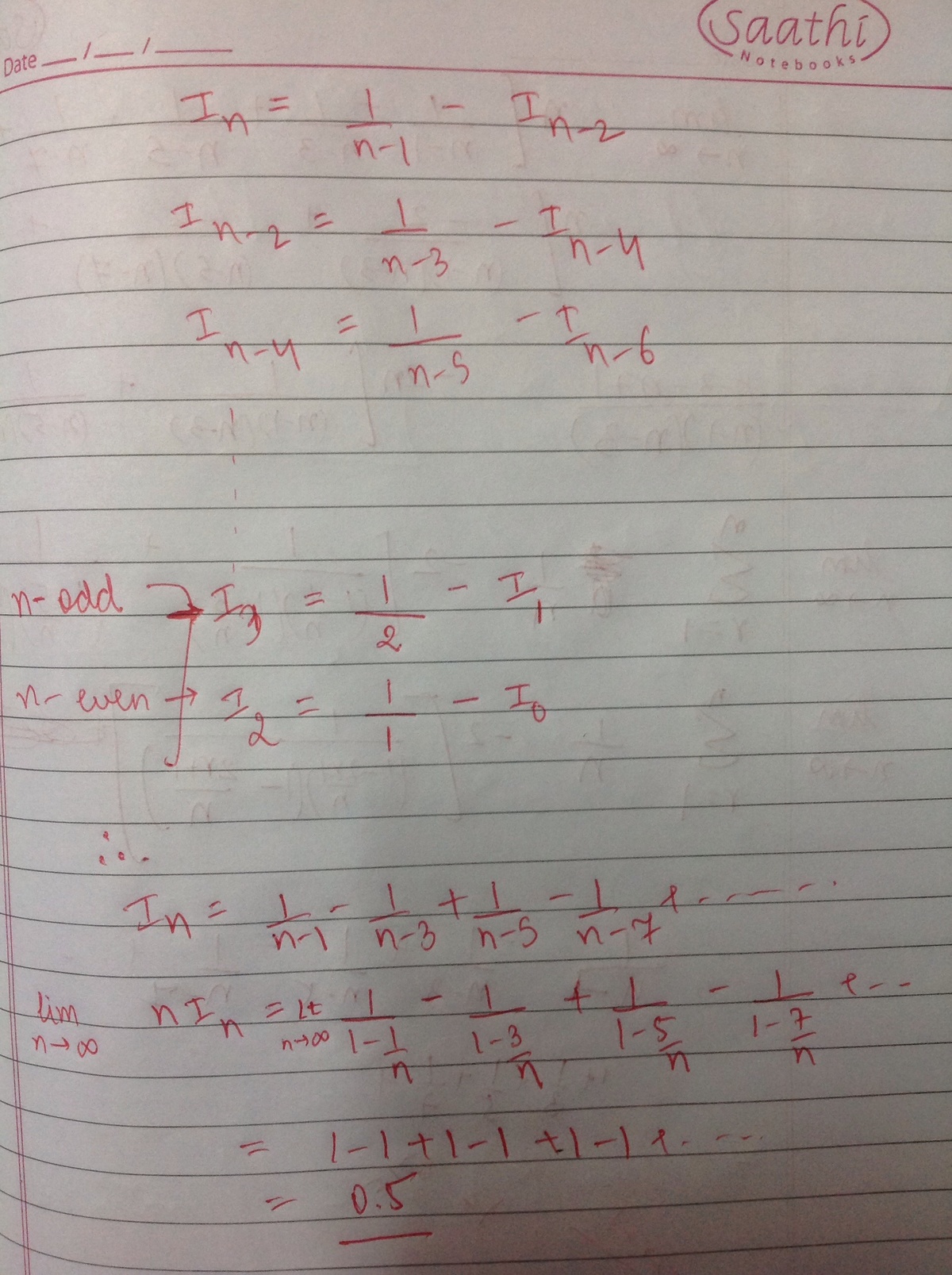
I have a query..is this last step correct? And if it isn't... doesn't the fact that the answer actually is 0.5 (see prakhar's solution) prove the last line to be correct?
Moderator note:
The last step is wrong. We cannot randomly interchange the order of limits. In this case,
n → ∞ lim ( i = 1 ∑ ∞ a i , n \neq \sum_i \lim_{n\rightarrow \infty} a_{i,n} \]
This is true if and only if certain conditions hold.
Let's calculate the integral first:- I n = ∫ 0 4 π t a n n x d x I n = ∫ 0 4 π t a n n − 2 x t a n 2 x d x I n = ∫ 0 4 π t a n n − 2 x ( s e c 2 x − 1 ) d x I n = ∫ 0 4 π t a n n − 2 x s e c 2 x d x − ∫ 0 4 π t a n n − 2 x d x I n = [ n − 1 t a n n − 1 x ] 0 4 π − I n − 2 I n + I n − 2 = n − 1 1 As n → ∞ , I n = I n − 2 = l ( l e t ) . Hence l + l = n − 1 1 l = 2 ( n − 1 ) 1 Now we will calculate the limit. n → ∞ lim 2 ( n − 1 ) n Hence the limit is 0 . 5 Please can anyone help me in solving the reduction formula so as to find the exact explicit formula of I n .