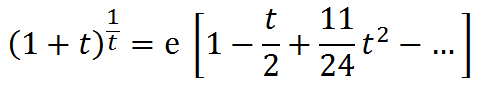Limits can be so unscrupulous

Or you can use the series

This can be done by using L'Hopital rule repeatedly. First we find the derivative of $(1+x)^{1/x}$ . Here, I don't show you, but you can try by taking $y=(1+x)^{1/x}$ and differentiate the equation $\log y=\frac{1}{x}\log(1+x)$ . Since the limit is of the indeterminate form $0/0$ , we take derivative and get $\lim_{x \to 0} \left[\frac{1}{x(x+1)}-\frac{1}{x^2}\log(1+x)\right](1+x)^{1/x} = \lim_{x \to 0} \left[\frac{x-(x+1)\log(1+x)}{x^2(x+1)}\right] \cdot (1+x)^{1/x}.$ What I'll show is that limit as $x \to 0$ of the expression in the bracket is $-1/2$ , so that I can split the limit into product of two limits $^{(*)}$ . $\begin{aligned} \lim_{x \to 0} \frac{x-(x+1)\log(1+x)}{x^2(x+1)} &= \lim_{x \to 0} \frac{-\log(1+x)}{3x^2+2x}\\ &= \lim_{x \to 0} \frac{-1/(1+x)}{6x+2}\\ &= -\frac{1}{2}. \end{aligned}$ Note that in each step, except the last one, it is of the form $0/0$ , so that we can take derivative on both part. Additionally, by substituting $n=1/x$ in the definition of $e$ , we see that $\lim_{x \to 0^+} (1+x)^{1/x}=e$ . Therefore, the answer is $-\frac{e}{2} \approx -1.4$ .

$^{(*)}$ If the limit is of the form $\lim f(x) \cdot g(x)$ , we need to show FIRST that both $\lim f(x)$ and $\lim g(x)$ exist. Then we can conclude that $\lim f(x) \cdot g(x) = \big(\lim f(x)\big) \cdot \big(\lim g(x)\big)$ .