Question posed by my peruvian teacher of calculus
L = x → 1 lim 1 − x 3 x − x
If L can be expressed as b a , where a , b are coprime positive integers, what is the value of a + b ?
Remark : try not to use L'Hôpital's rule.
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Discussions for this problem are now closed
Let x = y 6 , then:
\(\begin{array} {} L & = \displaystyle \lim_{x\rightarrow 1} \dfrac {\sqrt [3] {x} - \sqrt{x}}{1-x} = \displaystyle \lim_{y\rightarrow 1} \dfrac {y^2 - y^3}{1-y^6} \\ & = \displaystyle \lim_{y\rightarrow 1} \dfrac {y^2(1 - y)}{(1-y)(1+y+y^2+y^3+y^4+y^5)} \\ & = \displaystyle \lim_{y\rightarrow 1} \dfrac {y^2}{1+y+y^2+y^3+y^4+y^5} = \frac{1}{6} \end{array} \)
⇒ a + b = 1 + 6 = 7
Moderator note:
Nicely done. To clarify, you should mention why you let x = y 6 , which is because lcm ( 2 , 3 ) = 6 . Else, you would have gotten stuck solving for limits like this: x → 1 lim 1 − x x + 3 x − 7 x − 1 1 x .
As the (Numerator & Denominator) → 0 as x → 1 , we can use L-Hopital's Rule. Using the L-Hopital Rule, we get
L = x → 1 lim 1 − x x 3 1 − x 2 1
= x → 1 lim − 1 3 x 3 − 2 − 2 x 2 1 = 6 1 = b a
⇒ a + b = 1 + 6 = 7
P.S.
L- Hopital's Rule at a glance: In its simplest form, L'Hôpital's rule states that for functions f and g which are differentiable on an open interval I except possibly at a point c contained in I:
If
x → c lim f ( x ) = x → c lim g ( x ) = 0 or ± ∞ , and x → c lim g ′ ( x ) f ′ ( x ) exists, and g ′ ( x ) = 0 for all x in I with x ≠ c, then
x → c lim g ( x ) f ( x ) = x → c lim g ′ ( x ) f ′ ( x ) .
Source: Wikipedia. Thanks for patiently observing.
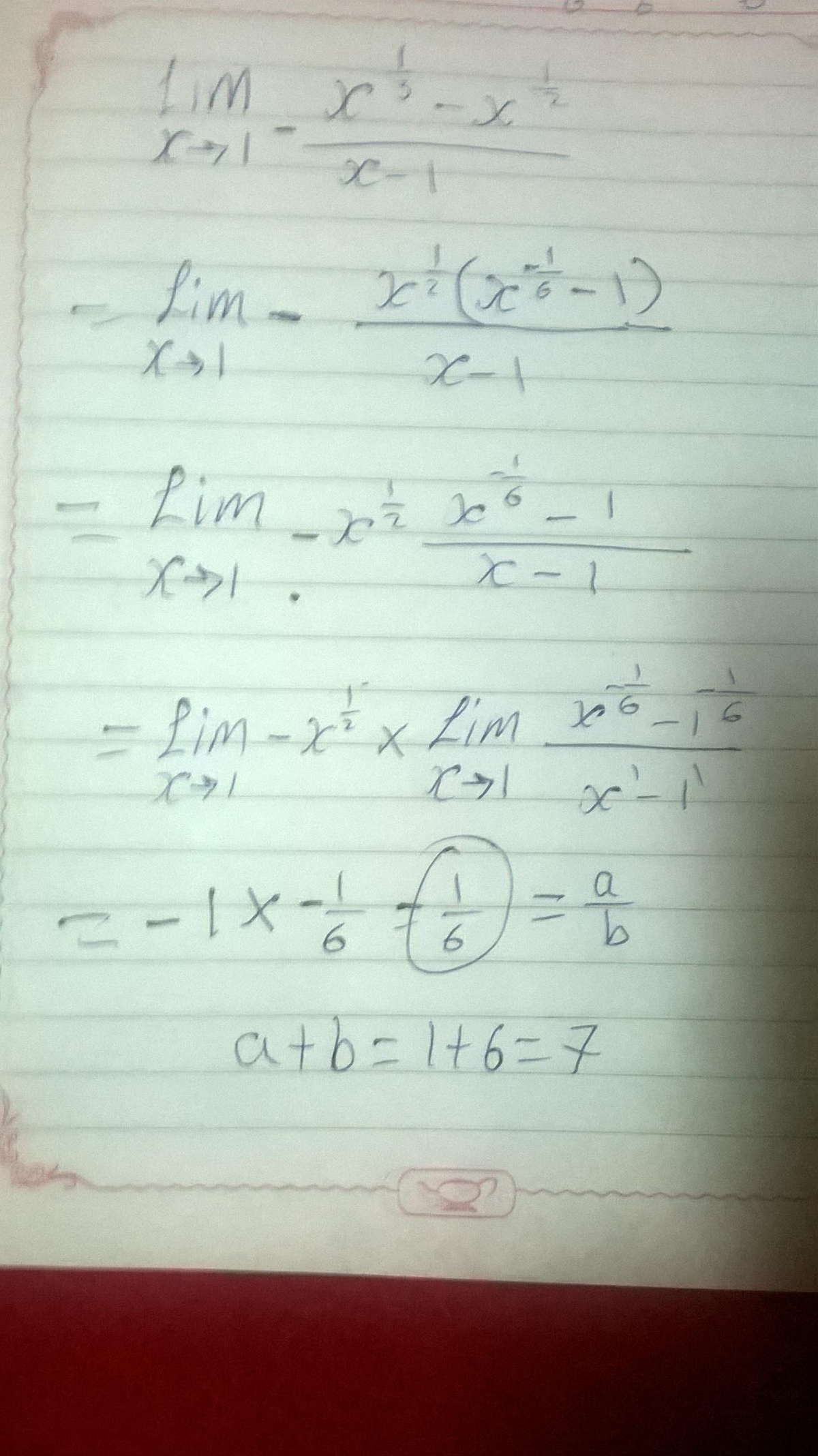
Factoring it out, we have:
L = x → 1 lim 3 x ⋅ 1 − x 1 − 6 x
With variable substitution, comes:
t = 6 x ⟹ L = t → 1 lim t 2 ⋅ 1 − t 6 1 − t
From the sum of terms on a geometric progression, we know:
1 − t 1 − t 6 = 1 + t + t 2 + t 3 + t 5 + t 6
Thus, we have:
L = t → 1 lim 1 + t + t 2 + t 3 + t 5 + t 6 t 2
Utilizing the limits' property that L = x → x 0 lim g ( x ) f ( x ) = g ( x 0 ) f ( x 0 ) , when both functions are polynomials, we get:
L = t → 1 lim 1 + t + t 2 + t 3 + t 5 + t 6 t 2 = 1 + 1 + 1 2 + 1 3 + 1 5 + 1 6 1 2 = 6 1
Hence, a + b = 7 .