Lindsay's shape
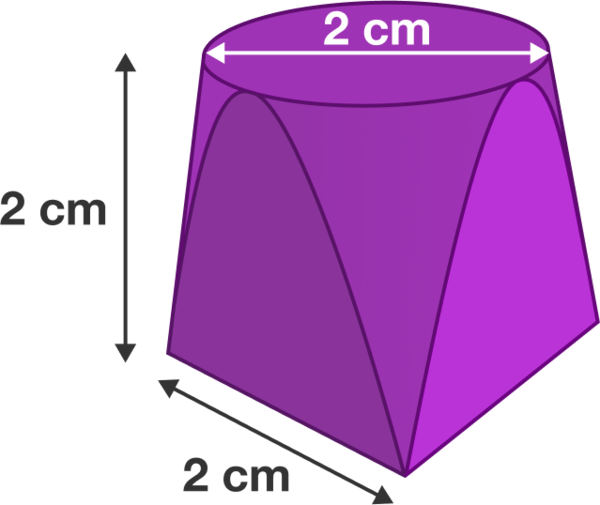
After studying various 3D shapes and finding formulas for their volumes, I challenged my students to invent a new shape. Lindsay created a shape ( with height 2 cm ) that is circular at the top ( with radius 1 cm ) but square at the bottom ( with side length 2 cm ) . Lindsay created this shape from a paraboloid: sliced four times parallel to the paraboloid's axis and two times perpendicular to the paraboloid's axis. Lindsay's shape is pictured below.
Find the volume of Lindsay's shape in cm 3 , which can be written as B A + C π with A , B , C integers, A and B coprime, and B positive.
Give the value of A + B + C .
The answer is 34.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
This solution critically depends on the fact that y = 2 x , which makes it impossible that the surface of revolution portion of Lindsay's shape is a cone. As Mark Hennings pointed out, it would be a paraboloid, not a cone. Had the segments been cut off from a conical fustrum, then the curve would not be a parabola, but a hyperbola.
See Conic Sections
Log in to reply
I can assure you the curved portion is a cone. I made it using tinkercad by taking 5 slices off a cone. The first slice is horizontal and makes the top a circle. The other four are vertical and define the square base.
My solution does have an error!! I literally just noticed. The side view should be a hyperbola, not a parabola. I'm holding a 3-d printed model and it sure looks like a parabola, but since the cut is parallel to the central axis, its a hyperbola.
EDIT: the solution works fine but for a shape that is different than the one I had in mind.
Go with it!
6 hours and several failed attempts later, I finally got it right - shockingly, only about 60 people have attempted an answer to this question in the 6 days it's been up so far. Very cool problem Jeremy! Thanks for the challenge.
the height of each triangle is 1 not 2
I divided the problem in two parts. The first was integrating the height of the paraboloid over the Interval [ − 1 : 1 ] 2 The height of the Paraboloid is z 1 =4-2*( x 2 + y 2 ) The result of this integral is 3 3 2
Then from this volume, I substracted the paraboloid that would sit on top of the circle. Defining the z 2 = 0 point of this volume at the top of the circle the height of the Paraboloid is z 2 =2-2* r 2 . Integrating in radial coordinates over [ 0 ; 2 π ] × [ 0 ; 1 ] this Volume is equal to π
The volume of the3D shape is then equal to 3 3 2 − π
So A=32; B=3; C=-1 and A+B+C= 3 4
This is amazing
I did something similar, but I calculated the first integral over [0, 1]² to make the calculation simpler, taking advantage of symmetry, and then multiplied by 4.
Very nicely done. I wish I had seen the integration this way. I got the answer but the integrals were messy and without Wolfram to do them for me I might have given up.
I first tried to find the equation of the parabola you would rotate around the y-axis to create the paraboloid. Here's an aerial view of the solid.

The bigger circle would be the base of the paraboloid after the first cut perpendicular to the axis, the square is the base after the four cuts parallel to the axis, and the inner circle is the top of the solid after the second perpendicular cut.
Assume the y-axis is the paraboloid's axis. Since the circle has a diameter of 2, the radius would be 1, and the distance from the center to the vertex of the square is 2 . This would represent the x-intercept of the parabola that would need to be rotated. Additionally, since the solid has a height of 2 units at the edge of the circle (a distance of 1 unit from the center), the parabola would have the point ( 1 , 2 ) . The parabola, with vertex on the y-axis, would have the equation y = a x 2 + k . Using the points ( 2 , 0 ) and ( 1 , 2 ) to solve for a and k , you get a = − 2 and k = 4 .

Integrating the right side of the parabola with respect to y (use the equation x = − 2 1 y + 2 ) from 0 to 2 will produce a solid paraboloid with the circular top that Lindsay's solid has.
∫ 0 2 − 2 1 y + 2 d y = 3 π
Now to find the volume of the solids that need to be cut off parallel to the paraboloids axis, I used an accumulating cross-section (building parabolas on the area between the bigger circle and the square if you look at the aerial picture). Assuming p is some value on the interval of ( 1 , 2 ) , the vertex of each parabola would have a height h = − 2 p 2 + 4 . The x-intercepts would be the "height" of the circle, which would be 2 − p 2 . The equation of each parabola ends up being y = − 2 x 2 − 2 p 2 + 4 (you can get this by using the general form y = a x 2 + k with k being the the height we found earlier and substituting the point ( 2 − p 2 , 0 ) for x and y to solve for a ).
To find the area under each parabola, I doubled the integral of y = − 2 x 2 − 2 p 2 + 4 with respect to x from 0 to 2 − p 2 . This gives you 3 8 ( 2 − p 2 ) 2 3 . Since this represents the area of each parabola, we can integrate to sum them up from 1 to 2 .
There are four of these parabolic solids we have to "slice off", so we'll calculate total area lost. The values of p are actually x-values on the parabola we originally revolved around the y-axis, so we can integrate 4 ∫ 1 2 3 8 ( 2 − x 2 ) 2 3 d x . The result is 4 π − 3 3 2 .
The total volume of Lindsay's solid is 3 π − ( 4 π − 3 3 2 ) = 3 3 2 − π .
A = 3 2 , B = 3 , C = − 1 , so the sum of all three is 34.
The equation of a paraboloid is z = x 2 / a 2 + y 2 / b 2 . When the cross-section is a circle, a = b , so the equation becomes C z = x 2 + y 2 . The circular cross-section of radius 1 occurs when C z = 1 , and the square cross-section has corners ( x , y ) = ( ± 1 , ± 1 ) , which gives C z = 2 . So the corresponding z -coordinates are 1 / C and 2 / C . The difference between them, which is 1 / C , is the height, which is 2 , so C = 1 / 2 and our equation becomes z = 2 ( x 2 + y 2 ) . So our solid is the paraboloid z ≥ 2 ( x 2 + y 2 ) cut by the six planes x = ± 1 , y = ± 1 , z = 2 , z = 4 . (In this formulation, the square cross-section is on top and the circle is on the bottom.)
The volume is the integral ∫ ∫ R h ( x , y ) d y d x where R is the plane region − 1 ≤ x , y ≤ 1 , and h is the vertical height of the solid above ( x , y ) . When x 2 + y 2 ≤ 1 , we get h ( x , y ) = 2 (this is the cylinder running through the middle of the solid). When 1 ≤ x 2 + y 2 ≤ 2 , we get h ( x , y ) = 4 − 2 ( x 2 + y 2 ) . The volume of the cylinder is 2 π and the volume of the second part can be split into four parts by symmetry, one for each quadrant of the x y -plane.
So we get 2 π + 4 ∫ ∫ S ( 4 − 2 x 2 − 2 y 2 ) d y d x where S is the region in the first quadrant bounded by x 2 + y 2 = 1 , x = 1 , y = 1 . This equals 2 π + 4 ∫ 0 1 ∫ 1 − x 2 1 ( 4 − 2 x 2 − 2 y 2 ) d y d x = 2 π + 4 ∫ 0 1 ( ( 4 − 2 x 2 ) ( 1 − 1 − x 2 ) − 3 2 + 3 2 ( 1 − x 2 ) 3 / 2 ) d x . Splitting this up and making the substitution x = sin θ , d x = cos θ d θ gives 2 π + 4 ∫ 0 1 ( 3 1 0 − 2 x 2 ) d x − 4 ∫ 0 π / 2 ( 4 − 2 sin 2 θ ) cos 2 θ d θ + 3 8 ∫ 0 π / 2 cos 4 θ d θ which equals 2 π + 3 3 2 − 1 6 ∫ 0 π / 2 cos 2 θ d θ + 8 ∫ 0 π / 2 sin 2 θ cos 2 θ d θ + 3 8 ∫ 0 π / 2 cos 4 θ d θ and these trigonometric integrals are well-known enough that I'll leave them to you; we end up getting 2 π + 3 3 2 − 4 π + π / 2 + π / 2 = 3 3 2 − π . So the answer is 3 2 + 3 − 1 = 3 4 .
The right-hand picture is a side view of the shape. It is a 2 c m square with a parabola inside it with the equation y = 2 x The vertical line is at a distance x from the left edge. The cyan lines transfer over to the left-hand picture which is a cross-section The blue triangle has a base of 2 ∗ 2 x and height 1 and there are 4 of them for a total area of 4 ∗ 2 x
The angle in each triangle is 2 ∗ arctan 2 x which means the leftover area for the sectors is 2 π minus 4 of these.
The radius of the sectors is 2 x + 1
The total area of the sectors is then ( 1 − π 4 arctan 2 x ) π ( 2 x + 1 )
The cross-section area function is then f ( x ) = ( 1 − π 4 arctan 2 x ) π ( 2 x + 1 ) + 4 ∗ 2 x
And so the volume is given by
∫ 0 2 f ( x ) d x
Which can be tackled in 4 pieces
∫ 0 2 π ( 2 x + 1 ) d x − ∫ 0 2 2 x arctan 2 x d x − ∫ 0 2 4 ∗ arctan 2 x d x − ∫ 0 2 4 ∗ 2 x d x
= 3 π − 3 8 − 4 ( π − 2 ) + 3 1 6
= 3 3 2 − π
So A = 3 2 , B = 3 , C = − 1 , A + B + C = 3 4