Loyal Lines

Probability Level 5

Given an $N$ -gon, we say that a line is loyal if it intersects the perimeter of the $N$ -gon along the entire length of exactly one edge. Determine the largest integer $N$ such that every non-degenerate $N$ -gon has a loyal line.

Details and assumptions

An $N$ -gon is non-degenerate if no three consecutive vertices are collinear, or equivalently, that no two consecutive edges are on the same line.
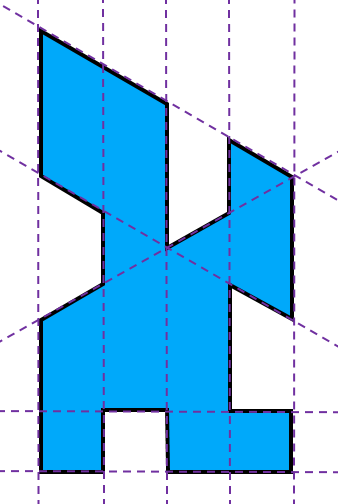
The above image is an example of a 20-gon that doesn't satisfy the conditions of the problem. The 10 dotted lines are all the lines that contain at least one edge of the 20-gon, however, because all of these lines contain 2 edges, none of them are loyal lines. This shows that the answer is not 20.

The answer is 13.

3 solutions

Matt McNabb
Aug 28, 2013

If $N \ge 10$ and $N$ is even then we have a simple counterexample: the outside of the $\frac{N}{2}$ -pointed star. For example N=10 .

The cases of $N$ being odd are a bit more problematic. If every line coincides with an even number of edges, then the total number of edges must be even. Therefore in this case there must be a line coinciding with an odd number of edges.

The minimal necessary case would be a line coinciding with $3$ edges. In this case there must be at least $6$ other lines (one through each endpoint of the 3 edges). Since these lines must each contain at least $2$ edges, there must be at least $15$ edges in the n-gon.

I was able to find a 15-gon counterexample; a modification of the pentacle star .

The same modification of the pentacle star that produced this, can be done on any of the other higher-pointed stars (adding 5 edges in total), so we have counterexamples for all $N \ge 14$ now, and have proven that $N=15$ is the smallest odd counterexample.

Therefore $N=13$ is the largest $N$ with no counterexamples.

There are a number of different stars, depending on how you try to join the vertices. If we fix the $2n$ -gon (for $n \ge 5$ ) to be the non-convex one obtained by trying to join vertex 1 to vertex 3, vertex 3 to vertex 5, and so on (so every attempted line misses out one vertex), then this $n$ -pointed star is indeed an example of a polygon with $2n$ sides for which no line exists containing just one edge.

Here is a systematic and relatively simple way of obtaining suitable examples of $m$ -gons with the desired property for all odd $m \ge 15$ . Start with the $2n$ -gon star where $n\ge6$ is even, and take a new point equidistant between two outer points of the star. Join that point to the two vertices (almost) diametrically opposite that point, and you obtain a $2n+3$ -gon with the desired properties:

alt text

Alternatively, join that point to one of the two vertices (almost) diametrically opposite that point and to a point on the line just "inside" the other (almost) diametrically opposite point, and you obtain a $2n+5$ -gon with the desired properties:

alt text

Between these two techniques, we get all $m$ -gons with $m\ge15$ and odd.

Mark Hennings - 7 years, 9 months ago

Very nice! I was constructing pointed stars and snipping off their tops instead.

Calvin Lin Staff - 7 years, 9 months ago

Another way of generating the odd cases $N=17$ and upwards is to draw the $(N-3)/2$ -pointed star, and then draw a line cutting off three of the points. Example with N=17

Matt McNabb - 7 years, 9 months ago

黎李
May 20, 2014

connecting ith and (i+2)th side of a convex n-gon to obtain an n-star shows N=2n is not right(n>=5) draw a butterfly (4 lines) on an equilateral triangle(3 lines) shows N=15 is not right, likewise N=17,19…… is not right if N=13, there must be a line having at least 3 segments, but that requires at least 6 addtional lines each having 2 segments, 6*2+3=15>13

Hariram K
Aug 28, 2013

First we will show that if the condition is false is not possible for some N, then it is not possible for N+2 as well.

For the condition to be not satisfied by a polygon, it must not be convex. So we can always find a line which cuts the polygon in four points. If only two vertices of the polygon are in one side, we cut the polygon along this line (like cutting a piece of that polygon shaped paper. look at the linked image for clarity). This new polygon would still satisfy the conditions and has 2 more sides. (I assumed that we can always find a polygon that can be cut with only two vertices on one side)

The linked image shows example of 10-sided and 15-sided polygon for which the condition is not true. By what I proved earlier, the condition is not true for 10+2m and 15+2m sided polygons for integer m. So it is not possible for 10, 12, 14, 15, 16, 17, .... Hence it appears that 13 is the largest value of N for which the condition gets met. All we need to show that there are no 13-gon violating the condition.

Since 13 is an odd number there must be at least one line which contains odd number of edges of our 13-gon. If our polygon has to violate the condition, each such line must have more than 1 edge. So it must have a line which has 3 edges. This line will have 6 collinear vertices of the polygon. There must be 6 more edges in the polygon each passing through one of these vertices. All these edges must be mutually non-collinear. They all must lie on a line which has more than 1 edge. So our polygon must have 6 more edges. Hence I have counted total 3+6+6 distinct edges which our odd-sided polygon must have in order to violate the conditions. So a 13-gon will always satisfy the condition.

"I assumed that we can always find a polygon that can be cut with only two vertices on one side" - I think this needs more work , for example the 20-gon in the question doesn't seem to have such a cut.

Matt McNabb - 7 years, 9 months ago

Agreed!

The diagrams that I worked with similar to Hariram's. Like you mentioned, the ability to "cut the polygon ... and has 2 more sides" has further conditions with regards to the gradients / slopes of the adjacent lines, and hence may not always continue.

I ended up having to construct a family of stars (similar to your comment "Example with $N=17$ >"). I do not believe that an inductive approach will work (in the sense of using the same base star and cutting more parts of it).

Calvin Lin Staff - 7 years, 9 months ago

Loyal Lines

The answer is 13.

3 solutions

0 pending reports