Line integral
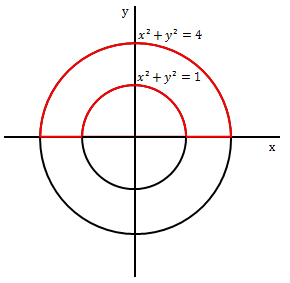
Let C be the region enclosed by the x -axis and the two circles x 2 + y 2 = 1 and x 2 + y 2 = 4 (as shown by the red curves in the figure).
What is the value of ∮ C ( y 2 d x + 5 x y d y ) ?
The answer is 14.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
is it possible to solve without polar coordinates
If I solve the question using cartesian coordinates while taking the path in counterclockwise direction, I am getting the answer as -14. Why is it so? Or am I doing any mistake?
Log in to reply
Without seeing your working, I would not be able to comment.
E.g. Are you certain that your path is counterclockwise? What happens when you compare your working to Kenny's solution below?
The direction we take matters since we are taking the integral with respect to x and y and not arc length. I also got -14 at first, going clockwise from the point (-2,0), so your solution should be correct.
I have two questions: 1. Why does the part after (3r Sin(Theta)) becomes r(dr)(d(Theta))? 2. I need to solve an exercise where they just give me one circle. Can i put it as x^2 + y^2 =16 (the equation they gave to me) and x^2 + y^2 = 0? (let's suppose we have a circle with a nule radius) I mean, can i opperate it as the area between those circumferences?
Log in to reply
- That's the change of variables to polar coordinates. Specifically, ∫ 1 d x d y = ∫ r d r d θ .
Yes, you could treat this as an integral of the bigger semicircle minus the smaller semicircle. That's essentially what Kenny did below.
Log in to reply
This article actually worked for me. I put it as a reference in a work for my university. Thanks, dude!
Here's for peeps like me who don't know nothing about Green's theorem .
Break down the integral into four parts, starting from (2,0), going in the anti-clockwise direction.
I 1 :
Parametrize as x = 2 cos θ and y = 2 sin θ .
We have d x = − 2 sin θ d θ and d y = 2 cos θ d θ .
I 1 = ∮ C ( y 2 d x + 5 x y d y )
= ∫ 0 π [ ( 2 sin θ ) 2 ( − 2 sin θ d θ ) + 5 ( 2 cos θ ) ( 2 sin θ ) ( 2 cos θ d θ ) ]
= ∫ 0 π ( − 8 sin 3 θ + 4 0 cos 2 θ sin θ ) d θ
= ∫ 0 π ( 4 0 sin θ − 4 8 sin 3 θ ) d θ
= 1 6
I 2 :
Since y is always 0 , so is the integral.
I 2 = 0
I 3 :
Parametrize similarly as I 1 to obtain:
I 3 = ∫ π 0 [ sin 2 θ ( − sin θ d θ ) + 5 ( cos θ ) ( sin θ ) ( cos θ d θ ) ]
Compare with I 1 :
I 3 = − 8 1 I 1 = − 2
I 4 :
Since y is always 0 , so is the integral.
I 4 = 0
Therefore ∮ C ( y 2 d x + 5 x y d y ) = 1 6 + 0 − 2 + 0 = 1 4 .
Good for people who don't know this skill!
By Green's theorem we get, ∮ C ( y 2 d x + 5 x y d y ) = ∫ ∫ A 3 y d A = 3 ∗ ( Area of figure enclosed ) ∗ y ˉ where y ˉ is the center of mass of the enclosed curve A .Given that center of mass of a semicircular disc is 3 π 4 R we can evaluate the center of mass of given closed curve by the principle of superposition. It turns out that y ˉ = 9 π 2 8 . Plugging in this value and the area of figure(which can be easily found out by subtracting the area of smaller semicircle from the bigger semicircle) we get the desired result.
Let P ( x , y ) = y 2 and Q ( x , y ) = 5 x y . By Green’s theorem, we have ∮ C ( P ( x , y ) d x + Q ( x , y ) d y ) = ∬ A ( ∂ x ∂ Q ( x , y ) − ∂ y ∂ P ( x , y ) ) , where C is the path and A is the area enclosed by the path. So, we have ∂ x ∂ Q ( x , y ) = 5 y , ∂ y ∂ P ( x , y ) = 2 y and ∂ x ∂ Q ( x , y ) − ∂ y ∂ P ( x , y ) = 5 y − 2 y = 3 y . Since the path is enclosed by two circles, we work in polar coordinates, where x = r cos θ , y = r sin θ with the limits 1 ≤ r ≤ 2 and 0 ≤ θ ≤ π . Substituting this in to the double integral, we have
∮ C ( y 2 d x + 5 x y d y ) = ∫ 0 π ∫ 1 2 ( 3 r sin θ ) r d r d θ = ∫ 0 π sin θ d θ ∫ 1 2 3 r 2 d r = [ − cos θ ] 0 π ⋅ [ r 3 ] 1 2 = 2 ⋅ 7 = 1 4