Line Segments Flying About
You are given four points and Suppose two line segments are to be constructed so that each point is used exactly once. What is the greatest possible distance between the midpoints of two such line segments?
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
It's best to arrange the points on a coordinate plane to get a sense of which segments will be farthest apart. Two configurations immediately stand out.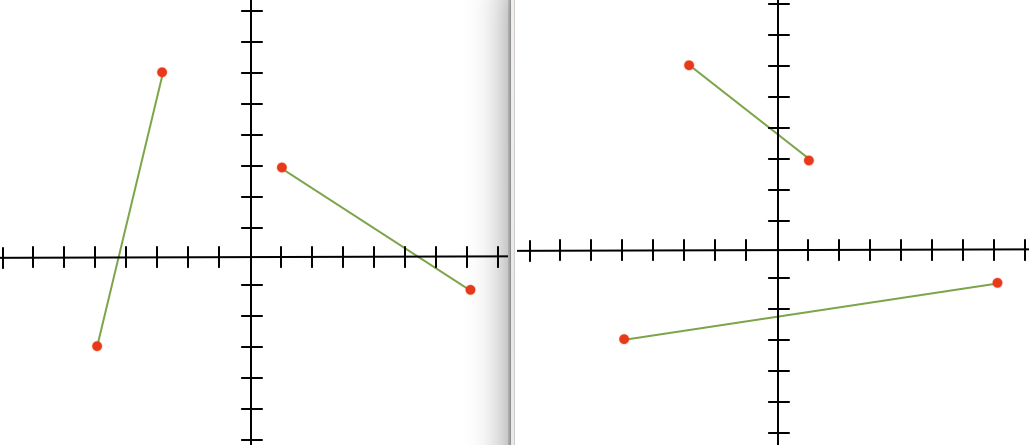
In the configuration on the left, the midpoints of each segment are ( − 4 , 1 ) and ( 4 , 1 ) , the distance between which is 8. In the configuration on the right, the midpoints of each segment are ( − 1 , 4 ) and ( 1 , − 2 ) , the distance between which is ( − 1 − 1 ) 2 + ( 4 − ( − 2 ) ) 2 = 4 + 3 6 = 2 1 0 , but this is less than 8, so the greatest distance created is 8.