line segments inside a square
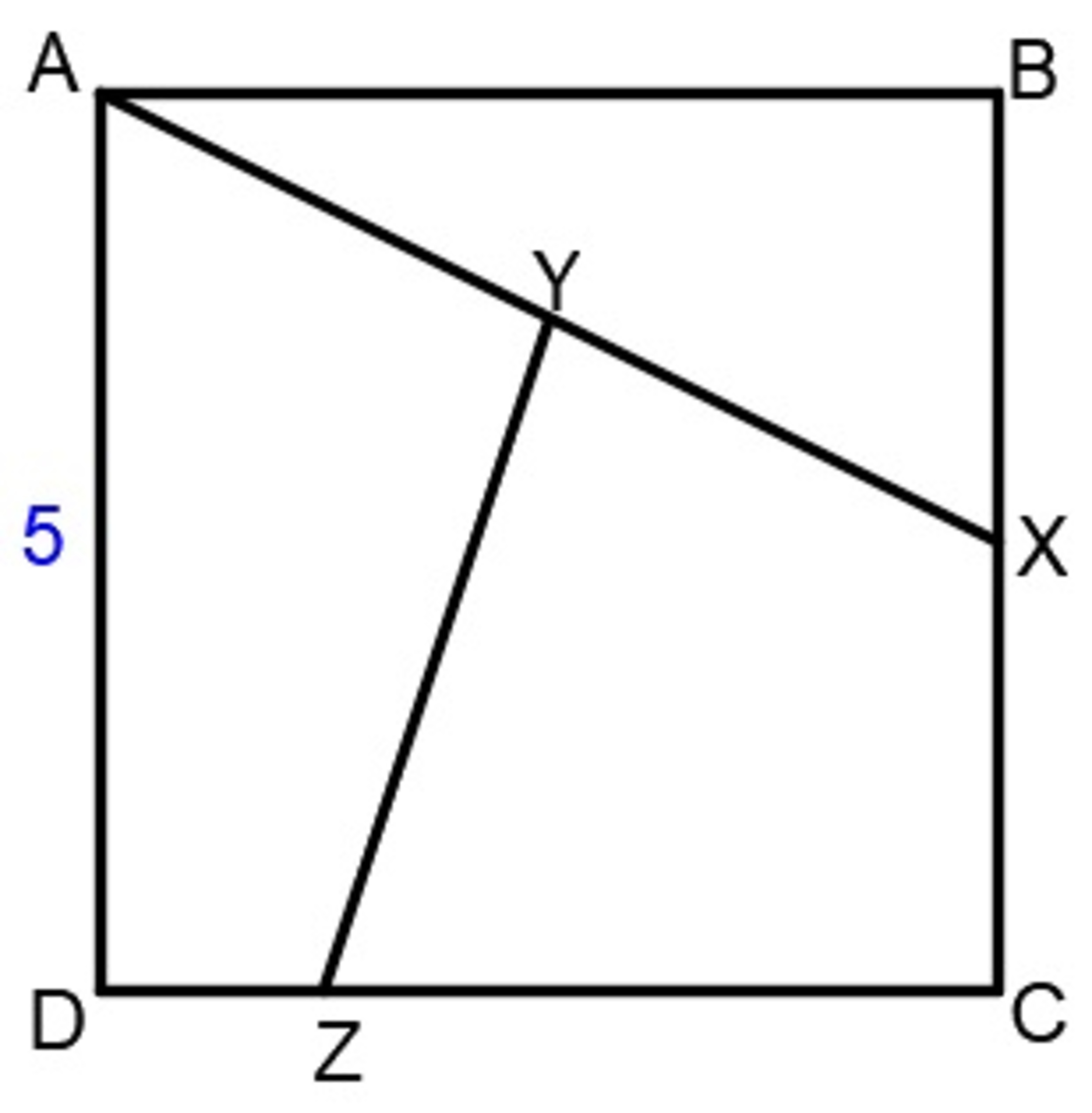In square
shown,
is the midpoint of
and
is the midpoint of
. If
and the side length of the square is
units, find
. If your answer can be expressed as
where
and
are positive coprime integers, give
.
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
We can solve this problem easily by using coordinate geometry with origin at D. So we can identify each point easily. We mention the results as follow. A(0,5),B(5,5),C(5,0),D(0,0),X(5,5/2),Y(5/2,5/4),Z(5/4,0). Then YZ can be found by using distance formula, YZ=5√10/4.This gives a+b=9