Equation in 2 variables
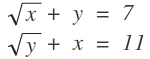 You think you rock at linear equation? Gimme the solution NOT using hit and trial method!
Solve for the values of "x" and "y" and enter
x
+
y
You think you rock at linear equation? Gimme the solution NOT using hit and trial method!
Solve for the values of "x" and "y" and enter
x
+
y
Note: These are not linear equations.
The answer is 13.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
If there're 1 more condition that x , y are square numbers, I will be able to do that.
Let a = x , b = y , so a , b are natural numbers.
a + b 2 = 7 (1')
a 2 + b = 1 1 (2')
(2') - (1'); a 2 − b 2 − a + b = 4
( a − b ) ( a + b ) − ( a − b ) = 4
( a − b ) ( a + b − 1 ) = 4
2 brackets multiply up to 4, 3 cases possible. (no negative cases because a + b − 1 is greater than 0.
- Case1: a − b = 1 , a + b − 1 = 4 we get a = 3 , b = 2
- Case2: a − b = 2 , a + b − 1 = 2 we get a = 2 5 , b = 2 1 (impossible)
- Case3: a − b = 4 , a + b − 1 = 1 we get a = 3 , b = − 1 (impossible)
So there's only 1 solution available x = 9 , y = 4 .
Synthetic division will do for factoring the equation.
I could not find a root of the quartic. I'm quite bad at that. Though good effort in that, You may see how I solved it.
Can we use determinants to solve this?
There is no need for synthetic divison because in the cubic part none
of the factors of 38 will satisfy and therefore no integer solution is
present. So the only solution which is integer is a = 3 => x = 9.
Log in to reply
The question didn't ask for only integer solutions, so I have to do some calculations to check if another non-integer solutions works.
Subtracting the two equations we get
y − x + x − y = − 4
( x − y ) ( x + y − 1 ) = 4 .
Now since x , y ∈ N , so
x + y > 1 → x ≥ y ( Since their product is positive ) .
So we need to check for two cases viz. ( x − y , x + y − 1 ) = ( 1 , 4 ) , ( 2 , 2 ) .
We can see that the latter doesn't yield integral solutions. So solving the former gives ( x , y ) = ( 9 , 4 ) .
So x + y = 1 3 .
Why x , y ∈ N ?
x + y = 7
=> y - 7 = x
=> ( y − 7 ) 2 = x
=> y 2 - 14y + 49 = x
Now, y + x = 11
=> y + ( y − 7 ) 2 = 11
=> y 2 - 14y + y + 38 = 0
Taking y = t
t 4 - 14 t 2 + t + 38 = 0
Applying remainder theorem
t = 2 will be one of the roots
So, (t - 2)( t 3 - 2 t 2 - 10t - 19) = 0
Again applying remainder theorem on the second part we can easily see that no integer will be the root as the constant term is a prime no. so it's factors will be only 1 and 19 or -1 and -19 which do not satisfy the 2nd part
This way only t = 2 is the integer solution so y = 4
and x = 9
Let a = x and b = y . The system then becomes: a + b 2 = 7 a 2 + b = 1 1
Subtract the equations: 1 1 − 7 = ( a 2 − b 2 ) − ( a − b ) ⟹ 4 = ( a − b ) ( a + b − 1 ) , which means that we either have ( a − b ) ⋅ ( a + b − 1 ) = 2 ⋅ 2 , which is not a solution to the system, or ( a − b ) ⋅ ( a + b − 1 ) = 1 ⋅ 4 , which is. This last case yields a = 3 and b = 2 , that is, x = a 2 = 9 and y = b 2 = 4 , so x + y = 1 3 .
Let\quad \sqrt { y } =t.\ So,\quad we\quad get\quad an\quad equation,\ { t }^{ 4 }-14.{ t }^{ 2 }+t+38=0.\ By\quad solving\quad the\quad quartic\quad equation\quad by\quad depressing\quad it,\ we\quad get\quad 2\quad positive\quad solutions\quad for\quad t.\ either\quad t=2\quad or\quad t=3.1313125\ But,\quad 7-{ t }^{ 2 }>0\ so,\quad t\quad cannot\quad be\quad more\quad than\quad 3,\ so\quad t=2,\quad y=4,\quad x=9\ Result:\quad x+y=13
I gave up doing normal stuffs we normally do, so my last effort is the brute force with little help from calculators. :<
From y + x = 1 1 (2)
y = 1 1 − x
Substitute into (1)
x 2 − 2 2 x + x + 1 2 1 = 7
Let a = x
a 4 − 2 2 a 2 + a + 1 1 4 = 0
( a − 3 ) ( a 3 + 3 a 2 − 1 3 a − 3 8 ) = 0
This right bracket degree 3 equation gives you 2 negative roots and 1 positive roots, which doesn't work on both equations for x and y. I tried by calculator, sorry. :(
So a = 3
x = 9
y = 4
Therefore, x + y = 1 3