Linear Regression
In Inferential Statistics,
linear regression
is a statistical tool to predict the behavior of a system based on the sample of data given.
It finds numerous applications in sales forecasting, quality control, inspection systems etc.
Linear Regression makes use of "linear relationship" between sample variables to predict the future outcome.
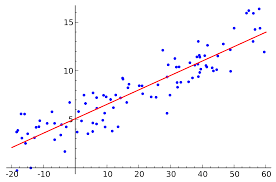 For a two variable regression,
we define the Line of Regression of
on
as:
where
are the means of
variables, respectively.
For a two variable regression,
we define the Line of Regression of
on
as:
where
are the means of
variables, respectively.
Also,
is the regression coefficient of y on
.
Similarly, we define the Line of Regression of
on
as:
Consequently,
is the regression coefficient of
on
In a partially destroyed laboratory record of an analysis of a
correlation
data, the variance
of
was found to be
.
Also, the Regression Equations were found to be:
If
denotes the variance of
then Calculate
and
Submit your answer as:
.
The answer is 34.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The two lines meet at the point ( 1 3 , 1 7 ) , and hence we have x = 1 3 and y = 1 7 . The two equations then become y − y = 5 4 ( x − x ) x − x = 2 0 9 ( y − y ) The standard theory of (least squares) linear regression tells us that σ x 2 C o v [ x , y ] = 5 4 σ y 2 C o v [ x , y ] = 2 0 9 where C o v [ x , y ] is the covariance of x and y , and hence σ x 2 σ y 2 = 9 1 6 so that (since σ x 2 = 9 ) the variance of y is σ y 2 = 1 6 , making the answer 1 3 + 1 7 + 1 6 = 3 4