Egyptian's way

Computer Science Level 2

An Egyptian fraction is a sum of positive distinct unit fractions. A fraction is unit fraction if numerator is 1 1 and denominator is a positive integer. Implement an algorithm to represent a fraction as the sum of finite unit fractions.

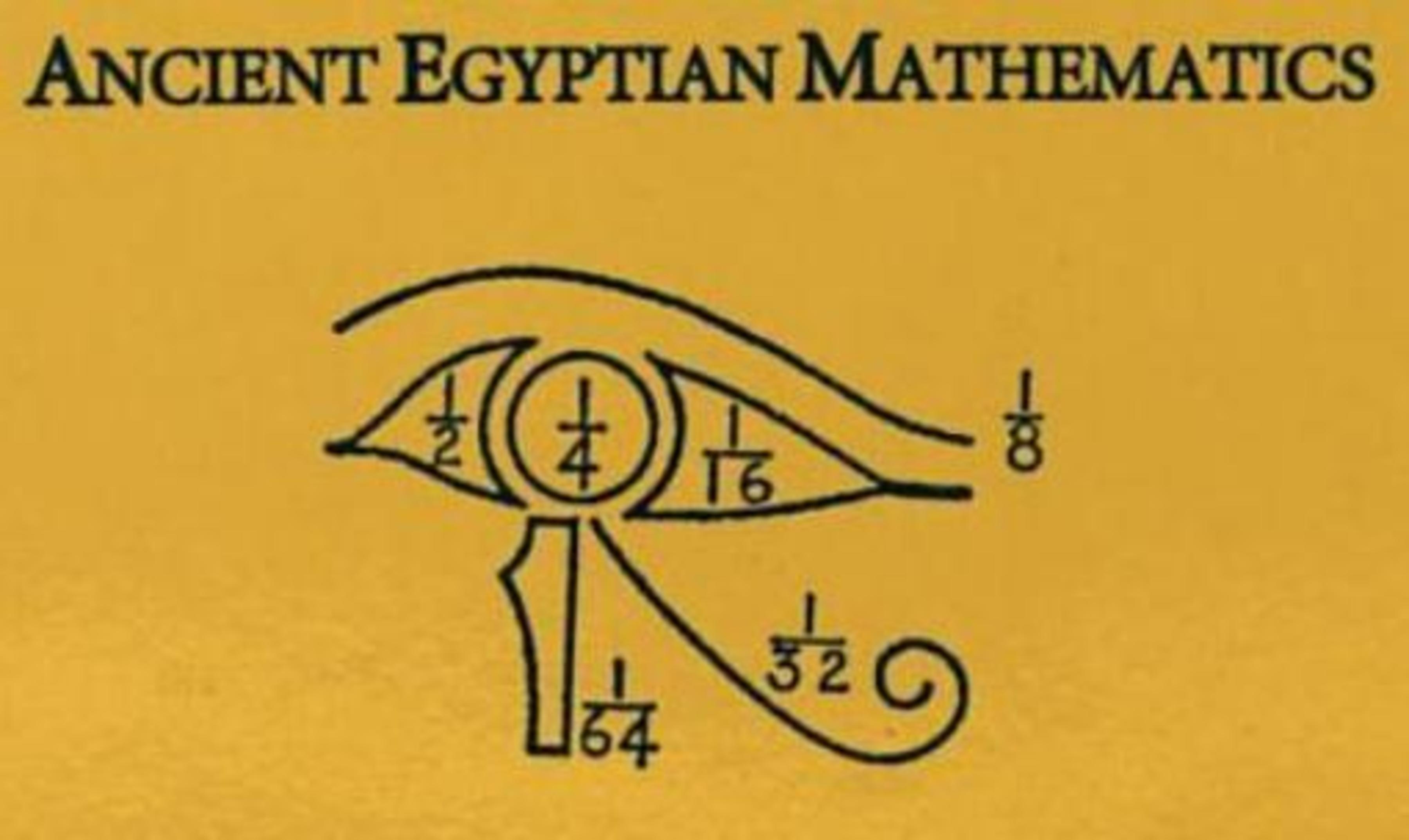
46 101 = 1 3 + 1 9 + 1 91 + 1 d \frac{46}{101}=\frac{1}{3}+\frac{1}{9}+\frac{1}{91}+\frac{1}{d}

What is the value of d d ?


The answer is 82719.

Beakal Tiliksew by Beakal Tiliksew , 24, Ethiopia

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Daniel Prime
Nov 6, 2015

Using a calculator that can simplify fractions, you find LHS to be reciprocal (82719) when solving for reciprocal(d). Hence, d = 82719.

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Ivan Koswara
Nov 5, 2015

Tip: This is not the way to ask someone to implement the algorithm. I just plugged to WolframAlpha , and technically I can just compute it by hand as well but I'm lazy. If you want to force to implement the algorithm, you can ask something like " 46 101 \frac{46}{101} can be represented as the sum of unit fractions; implement a greedy algorithm to do this (pick largest allowed fraction each time) and find the denominator of the smallest fraction".

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Bill Bell
Jul 31, 2015

Although I peered at Egyptian fraction only briefly it was enough to discourage me from creating an algorithm. Here's a quick answer to the problem given though. 

1
2
 
from fractions import Fraction as F
print F(46,101)-(F(1,3)+F(1,9)+F(1,91))

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...