This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
17 solutions
Those must be special pencils.
Log in to reply
If you get a very nice pencil (in the United States) they can run up to $70. $4 pencils are certainly possible.
Ah - in Japan there are legendary mangaka pencils they don't make anymore - maybe these are them!
Those are some expensive pencils.
4a+5b =32 5c+4d=31 e=3 Maybe instead of using the logic and variables I could have simply worked backwards. 6. I found this problem a little challenging but I decided not to give up until I figured out the process.
It's an unrealistic problem, given that the individual pencils cost more than individual books.
By adding one book and removing a pencil, the total price is $1 less. Repeat until no pencils are left and you have 9 books which total to $27. Divide to get the individual price of $3.
Moderator note:
This reflects an unusual approach to simultaneous equations as recursive definition.
That is, given 4 x + 5 y = 3 2 and 5 x + 4 y = 3 1 , rather than doing the usual trick of subtracting equations, we can just note what happens to the other two values when tracking 1 being subtracted from the y term between equations. Since this is an operation that can be iterated until 0 y , it suffices to remove the y term altogether.
Essentially, treating the equation as t x + r y = s , we have found the t , r , and s terms are fixed as 4 + 1 a , 5 − 1 a , and 3 2 − 1 a for any integer a .
A roughly similar idea can be found with writing the solution of a Diophantine equation; once knowing one solution ( x , y ) , we can write it in the form ( x + t a , y + r a ) for some integers t and r and any integer a to be able to recursively write every solution.
I've used this procedure with an assortment of these types of picture systems-of-equations problems. I've also used the concepts of weighted means (averages) and moments equilibrium (center of gravity) concepts to solve assorted mixture problems which are more classically (and tediously) solved with standard system-of-equations methods.
Could you explain what repeat means in your answer and how you would show it?
By removing a pencil and add in a book the total price is $1 lesser. Do this until there is no more pen left. Price/total of books= price of each book.
Relevant wiki: System of Linear Equations (Simultaneous Equations)
B = b o o k and P = p e n c i l
4 B + 5 P = 3 2 ⟹ 1
5 B + 4 P = 3 1 ⟹ 2
Method 1: Substitution Method
In 1 , solve P in terms of B then substitute in 2 .
4 B + 5 P = 3 2 ⟹ P = 5 3 2 − 4 B
5 B + 4 P = 3 1 ⟹ 5 B + 4 ( 5 3 2 − 4 B ) = 3 1 ⟹ 5 B + 5 1 2 8 − 5 1 6 B = 3 1 ⟹ 5 9 B = 5 2 7 ⟹ B = 3
Method 2: Elimination Method
( − 4 × 1 ) + ( 5 × 2 ) , we get
9 B = 2 7
B = 3
Method 3: By Determinants
B = ∣ ∣ ∣ ∣ 4 5 5 4 ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ 3 2 3 1 5 4 ∣ ∣ ∣ ∣ = ( 4 ) ( 4 ) − ( 5 ) ( 5 ) ( 3 2 ) ( 4 ) − ( 3 1 ) ( 5 ) = − 9 − 2 7 = 3
Ok... Facílimo!
Resolvemos esta questão através de um sistema de equação do 1º grau (com duas incógnitas) Chamarei o Livro de X e o Lápis de Y:
4x+5y = 32 (x4) e (x-1) ou (x-4) 5x+4y = 31 (x5)
-16x-20y = -128
25x+20y = 155
9x = 27 x=27/9 x=3
Log in to reply
@Antonio Araujo Correia This is the translated version
Ok ... Easy! We solve this question through a system of equation of the first degree (with two unknowns) I will call the Book of X and the Pencil of Y:
4x+5y = 32 (x4) and (x-1) or (x-4) 5x+4y = 31 (x5)
-16x-20y = -128
25x+20y = 155
9x = 27
x = 27/9
x=3
4 books and 5 pencils cost $32 while 5 books and 4 pencils cost $31 so adding them, we see that 9 books and 9 pencils cost $63, meaning a book and a pencil together cost $7. Then 4 books and 4 pencils cost $28 and we subtract this from 5 books and 4 pencils which cost $31, we see that 1 book costs $3.
Solution by elimination method:
Suppose b = price of a book and p = price of a pencil.
4 b + 5 p = 3 2 . . . . . . . . . ( 1 )
5 b + 4 p = 3 1 . . . . . . . . . ( 2 )
Multiply the first equation by 4 and multiply second equation by 5.
1 6 b + 2 0 p = 1 2 8
− 2 5 b − 2 0 p = − 1 5 5
After subtracting, we get
9 b = 2 7
b = 3
One book = $3 and One pencil = $4 4 ( $ 3 ) + 5 ( $ 4 ) = $ 3 2
5 ( $ 3 ) + 4 ( $ 4 ) = $ 3 1
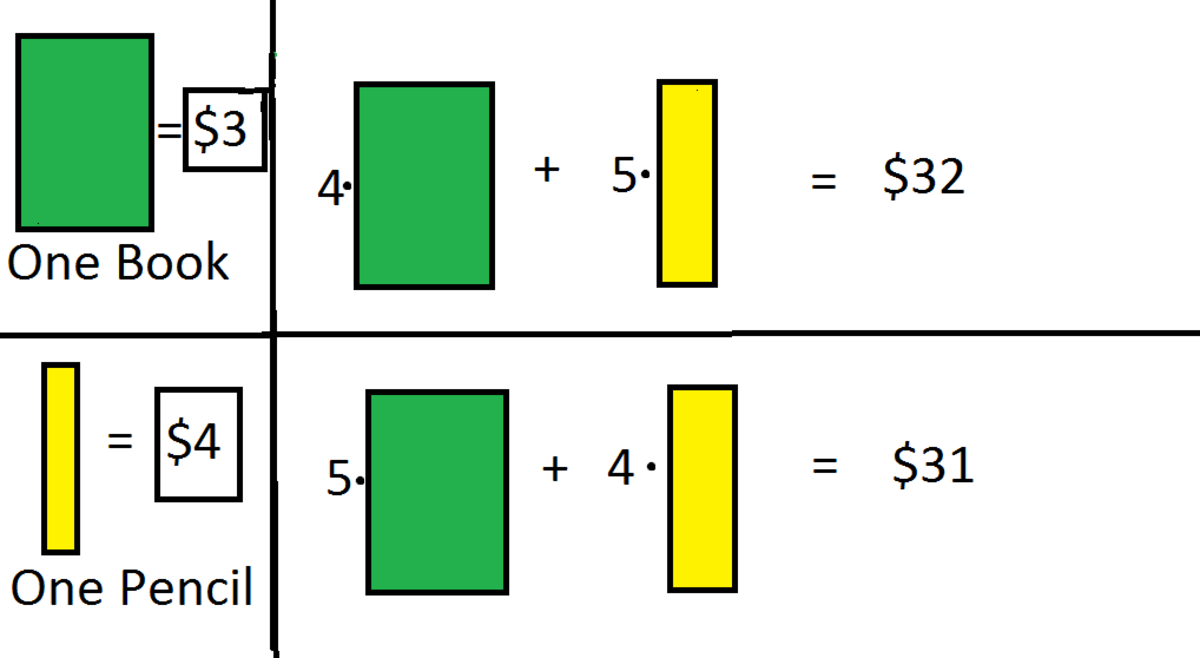
Yeah, but how do you get the book and pencil values?
At first I assume that one book = $3 and one pencil = $4
I saw ($3,$4) satisfy all of the equations.
4 ( $ 3 ) + 5 ( $ 4 ) = $ 3 2
5 ( $ 3 ) + 4 ( $ 4 ) = $ 3 1
A very math-looking approach then!
books = b and pencils = p .
( 4 5 5 4 ) ( b p ) ( b p ) = ( 3 2 3 1 ) = 4 ⋅ 4 − 5 ⋅ 5 1 ( 4 − 5 − 5 4 ) ( 3 2 3 1 ) = − 9 1 ( − 2 7 − 3 6 ) = ( 3 4 )
Therefore, one book costs $ 3 .
...and one pencil costs $ 4 , apparently. Damn, that's a one expensive pencil.
suppose,books=b and pencils=p
now, 4 b + 5 p = 3 2 .....................[1]
and 5 b + 4 p = 3 1 .......................[2]
now,multiplying [1] by 4 and multiplying [2] by 5 and then doing [2]-[1], we get that,
2 5 b + 2 0 p − 1 6 b − 2 0 p = 1 5 5 − 1 2 8
or, 9 b = 2 7
or, b = 3
so, the cost of a book is 3 $
4x + 5y = 32
5x + 4y = 31
Add both equations
9x + 9y = 63
9(x+y) = 63
x + y = 7
The answers are 2, 3, 4 or 9, we can rule out 9, since it's too big
1) if x =2 then y=5
4 * 2 + 5 * 5 = 33, so X ISN'T 2
2) if x=3 then y=4
4 * 3 + 5 * 4 = 32
also 5 * 3 + 4 * 4 = 31
The second equation contains an even number of pencils and an odd number of books which sum to an odd number. So the price of a book is odd. 9 is too large, so that leaves us with 3.
Hahah I done the same XD
Given that the answers are all whole numbers it is faster to just solve for 5, then 4 then 3 to find a solution.
All I want to add to previous solutions is: How does a pencil cost more than a book?!?
Add the two data - 9 of each cost $63, so one of each costs $7. Take 4 of each from the second datum: $(31-28) = $3 Ockham's razor?
By adding one book and removing one pencil you reduce the amount by $1.So if you remove all four pecils and add four more books that will reduce the amount in the second group by $4, to $27.So if 9 books cost $27,one book costs $3.
4b+5p=32$
5b+4p=31$
Difference between 1 book's value and 1 pen's value is 1$ in favour of pen
Sum up two equations
9b+9p=63$
1b+1p=7$
1b=3$
1p=4$
4b + 5p = 32
5b + 4p = 31
Note that in these kinds of problems with alrternating coefficients, a good first attempt is to directly add them which usually results in some sort of factoring allowing a "unit sum" to occur.
Result: 9b + 9p = 63
Factored: b + p = 7
Here can be noted that each coefficient is 1, ie a unit and multiplying will be an effective way to reduce an above alternating equation. As we're looking for b find the equation with more b than p.
Equation 2:
5b + 4p = 31
-(4b + 4p = 28)
b = 3.
The same could be done to find p.
First time posting, would love any criticism or comments.
It is not always necessary to solve simultaneous equations by following a set algorithm. Sometimes you can just see the answer by inspection, and sometimes you can exploit peculiar features of the equations. In this problem the interesting pattern of '5' and '4' leads to a quick solution -
Let b and p be the cost of a book and pencil respectively. Adding the two top rows together and dividing by 9 shows that
b + p = 7
Subtracting the top row from the second shows that
b − p = − 1
Adding these two equations gives
2 b = 6
And so
b = 3
Relevant wiki: System of Linear Equations (Simultaneous Equations)
4 b + 5 p = 3 2
5 b + 4 p = 3 1
Subtracting the second equation from the first, we get:
− b + p = 1
p = b + 1
Substituting into the first equation, we get:
4 b + 5 ( b + 1 ) = 3 2
9 b + 5 = 3 2
9 b = 2 7 ⇒ b = 3